Which Of The Following Is An Even Function
Juapaving
Apr 06, 2025 · 6 min read
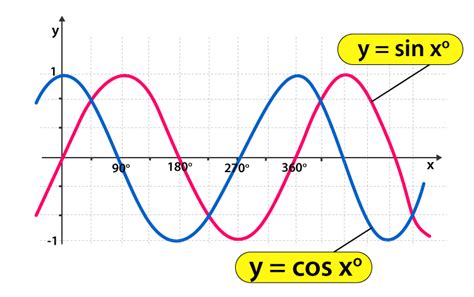
Table of Contents
Which of the Following is an Even Function? A Deep Dive into Even and Odd Functions
Understanding even and odd functions is crucial in various fields, including calculus, trigonometry, and signal processing. This comprehensive guide will explore the definitions, properties, and identification of even and odd functions, providing you with a robust understanding of the topic. We'll delve into practical examples and demonstrate how to determine whether a given function is even, odd, or neither.
What are Even and Odd Functions?
A function is a mathematical relationship that maps each input value (from its domain) to exactly one output value (in its codomain). Even and odd functions are specific types of functions characterized by their symmetry properties.
Even Function: A function f(x) is considered even if it satisfies the following condition:
f(-x) = f(x) for all x in the domain.
This means that if you replace x with -x, the function's value remains unchanged. Graphically, an even function is symmetric about the y-axis. This symmetry means that if you were to fold the graph along the y-axis, the two halves would perfectly overlap.
Odd Function: A function f(x) is considered odd if it satisfies the following condition:
f(-x) = -f(x) for all x in the domain.
Replacing x with -x results in the negative of the original function's value. Graphically, an odd function exhibits symmetry about the origin. This means that if you were to rotate the graph 180 degrees about the origin, it would remain unchanged.
Neither Even Nor Odd: Many functions don't possess either of these symmetries and are therefore classified as neither even nor odd.
Identifying Even and Odd Functions: A Step-by-Step Guide
Let's walk through a systematic approach to determining whether a function is even, odd, or neither.
-
Replace x with -x: This is the fundamental step. Substitute -x for every instance of x in the function's equation.
-
Simplify the Expression: After the substitution, simplify the resulting expression as much as possible.
-
Compare with the Original Function: Compare the simplified expression with the original function f(x).
- If the simplified expression is identical to f(x), the function is even.
- If the simplified expression is equal to -f(x), the function is odd.
- If neither of the above conditions holds, the function is neither even nor odd.
Examples of Even and Odd Functions
Let's illustrate this process with some examples:
Example 1: f(x) = x²
-
Substitute -x: f(-x) = (-x)² = x²
-
Compare: f(-x) = f(x)
Conclusion: f(x) = x² is an even function. Its graph is a parabola symmetric about the y-axis.
Example 2: f(x) = x³
-
Substitute -x: f(-x) = (-x)³ = -x³
-
Compare: f(-x) = -f(x)
Conclusion: f(x) = x³ is an odd function. Its graph is symmetric about the origin.
Example 3: f(x) = x² + x
-
Substitute -x: f(-x) = (-x)² + (-x) = x² - x
-
Compare: f(-x) ≠ f(x) and f(-x) ≠ -f(x)
Conclusion: f(x) = x² + x is neither even nor odd. Its graph lacks the symmetry of even or odd functions.
Example 4: f(x) = sin(x)
-
Substitute -x: f(-x) = sin(-x)
-
Simplify: Using the property sin(-x) = -sin(x), we get f(-x) = -sin(x)
-
Compare: f(-x) = -f(x)
Conclusion: f(x) = sin(x) is an odd function.
Example 5: f(x) = cos(x)
-
Substitute -x: f(-x) = cos(-x)
-
Simplify: Using the property cos(-x) = cos(x), we get f(-x) = cos(x)
-
Compare: f(-x) = f(x)
Conclusion: f(x) = cos(x) is an even function.
Example 6: f(x) = e<sup>x</sup>
-
Substitute -x: f(-x) = e<sup>-x</sup>
-
Compare: e<sup>-x</sup> ≠ e<sup>x</sup> and e<sup>-x</sup> ≠ -e<sup>x</sup>
Conclusion: f(x) = e<sup>x</sup> is neither even nor odd.
Example 7: f(x) = |x|
-
Substitute -x: f(-x) = |-x| = |x|
-
Compare: f(-x) = f(x)
Conclusion: f(x) = |x| is an even function. The absolute value function is symmetric about the y-axis.
Example 8: f(x) = 1/x
-
Substitute -x: f(-x) = 1/(-x) = -1/x
-
Compare: f(-x) = -f(x)
Conclusion: f(x) = 1/x is an odd function.
Properties of Even and Odd Functions
Even and odd functions possess several interesting properties:
-
Sum and Difference: The sum of two even functions is even, and the difference between two even functions is even. The sum of two odd functions is odd, and the difference between two odd functions is odd. However, the sum or difference of an even and an odd function is generally neither even nor odd.
-
Product: The product of two even functions is even. The product of two odd functions is even. The product of an even and an odd function is odd.
-
Composition: The composition of two even functions is even. The composition of two odd functions is odd.
-
Integration: The definite integral of an even function from -a to a is twice the integral from 0 to a. The definite integral of an odd function from -a to a is zero.
-
Derivatives: The derivative of an even function is odd, and the derivative of an odd function is even (assuming the derivative exists).
Applications of Even and Odd Functions
The concepts of even and odd functions are valuable in various areas:
-
Fourier Series: Fourier series decompose periodic functions into a sum of sines and cosines (which are odd and even functions, respectively). This decomposition simplifies the analysis and manipulation of complex periodic signals.
-
Signal Processing: In signal processing, even and odd functions are used to analyze and manipulate signals, separating them into symmetric and anti-symmetric components.
-
Quantum Mechanics: Even and odd functions play a significant role in quantum mechanics, particularly in the description of particle wave functions.
-
Physics and Engineering: Many physical phenomena and systems exhibit even or odd symmetry, making these function types essential tools for modeling and analysis.
Conclusion
Determining whether a function is even, odd, or neither involves a straightforward process of substitution and comparison. Mastering this skill is fundamental to a deeper understanding of mathematical functions and their applications in various fields. Remember the key characteristics: even functions are symmetric about the y-axis (f(-x) = f(x)), odd functions are symmetric about the origin (f(-x) = -f(x)), and those that don't meet either criteria are neither even nor odd. By understanding these properties and applying the step-by-step guide, you can confidently analyze and classify functions based on their symmetry. This understanding opens doors to more advanced concepts and applications within mathematics, science, and engineering.
Latest Posts
Latest Posts
-
How Many Electrons Are Being Shared In A Triple Bond
Apr 08, 2025
-
What Are The Coordinates Of Point J
Apr 08, 2025
-
What Is 20 Percent Of 600
Apr 08, 2025
-
Lcm Of 15 12 And 8
Apr 08, 2025
-
Moment Of Inertia For A Circular Cross Section
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Which Of The Following Is An Even Function . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.