Which Is More .25 Or .5
Juapaving
May 09, 2025 · 4 min read
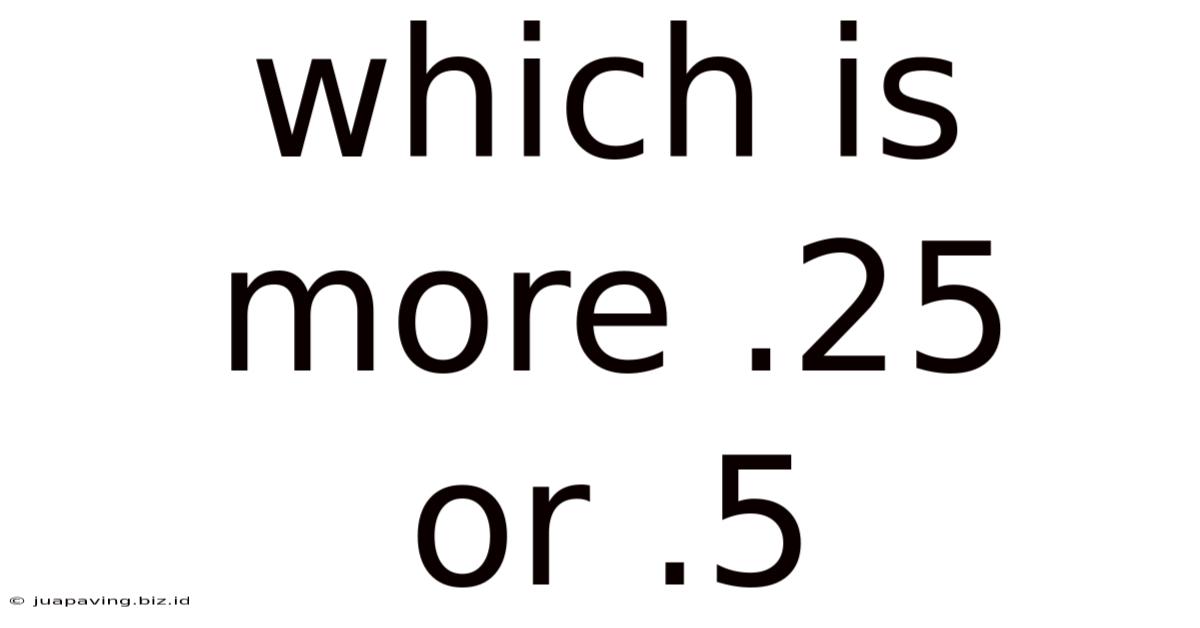
Table of Contents
Which is More: 0.25 or 0.5? A Deep Dive into Decimal Comparisons
The seemingly simple question, "Which is more: 0.25 or 0.5?", might seem trivial at first glance. However, a deeper exploration of this comparison opens the door to understanding fundamental concepts in mathematics, particularly decimal representation, fraction equivalence, and the importance of precise numerical comparisons. This article will not only answer the question directly but will also delve into the underlying principles, offering practical examples and applications to solidify your understanding.
Understanding Decimal Representation
Before directly comparing 0.25 and 0.5, let's establish a clear understanding of decimal representation. Decimals are a way of expressing numbers that are not whole numbers. The decimal point separates the whole number part from the fractional part. Each digit to the right of the decimal point represents a fraction of a power of ten.
- 0.1 represents one-tenth (1/10)
- 0.01 represents one-hundredth (1/100)
- 0.001 represents one-thousandth (1/1000) and so on.
Therefore, 0.25 can be understood as 2 tenths + 5 hundredths, or 2/10 + 5/100. Similarly, 0.5 represents 5 tenths, or 5/10.
Converting Decimals to Fractions for Easier Comparison
Converting decimals to fractions often simplifies comparisons. This approach allows us to visualize the numbers and their relative sizes more effectively.
-
0.25 as a fraction: 0.25 = 25/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 25. This simplifies to 1/4.
-
0.5 as a fraction: 0.5 = 5/10. Again, simplifying this fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 5, gives us 1/2.
Now the comparison becomes: Which is more, 1/4 or 1/2? Visually representing these fractions as parts of a whole makes the comparison intuitive. If you imagine a pie cut into four equal slices (1/4), one slice is smaller than if the same pie is cut into two equal slices (1/2). Therefore, 1/2 is larger than 1/4.
Visualizing the Comparison using a Number Line
Another effective method for comparing decimals is by visualizing them on a number line. A number line is a visual representation of numbers, ordered from least to greatest. Plotting 0.25 and 0.5 on a number line clearly shows that 0.5 lies to the right of 0.25, indicating that 0.5 is greater.
Understanding Place Value and Magnitude
The place value system in decimals is crucial for understanding magnitude. In the numbers 0.25 and 0.5, the tenths place holds the most significant value. 0.5 has a 5 in the tenths place, while 0.25 has a 2 in the tenths place. Since 5 is greater than 2, 0.5 is greater than 0.25. The hundredths place in 0.25 is irrelevant to the comparison because the difference in the tenths place is significant enough to determine which number is larger.
Real-World Applications: Practical Examples
The comparison between 0.25 and 0.5 has numerous real-world applications. Here are a few examples:
1. Measurements and Quantities:
Imagine you have two containers. One contains 0.25 liters of liquid, and the other contains 0.5 liters. Clearly, the second container holds more liquid.
2. Financial Calculations:
If you have two discounts offered: a 0.25 (25%) discount and a 0.5 (50%) discount, the 50% discount will save you more money.
3. Data Analysis and Statistics:
In statistical analysis, comparing proportions or percentages often involves decimal comparisons. For instance, if two groups show success rates of 0.25 and 0.5 respectively, the second group displays significantly higher success.
4. Scientific Measurements:
In many scientific fields, measurements are expressed using decimals. Comparing quantities such as the mass of objects, the length of specimens, or the volume of substances frequently involves comparing decimal numbers.
Advanced Concepts and Extensions:
The comparison between 0.25 and 0.5 lays the groundwork for understanding more complex concepts:
-
Percentage Calculations: Understanding decimals is fundamental to calculating percentages. 0.25 represents 25%, and 0.5 represents 50%.
-
Ratio and Proportion: These concepts are closely related to fractions and decimals. The ratio of 0.25 to 0.5 is equivalent to the ratio of 1/4 to 1/2, which simplifies to 1:2.
-
Algebra and Equations: Solving equations often requires manipulating decimal numbers. Understanding their relative magnitudes is essential for correctly solving these equations.
Conclusion: 0.5 is Greater than 0.25
To reiterate, the answer to the question, "Which is more: 0.25 or 0.5?" is unequivocally 0.5. This seemingly simple comparison highlights the importance of understanding fundamental mathematical concepts such as decimal representation, fraction equivalence, place value, and visualization techniques. By mastering these concepts, you develop a stronger foundation for tackling more complex mathematical problems and real-world applications that involve numerical comparisons. The ability to confidently and accurately compare decimal numbers is a valuable skill across diverse fields, from everyday calculations to advanced scientific research. Remember that a solid understanding of these basic numerical concepts is the bedrock for success in more advanced mathematical pursuits.
Latest Posts
Latest Posts
-
Are All Ionic Compounds Soluble In Water
May 10, 2025
-
Lcm Of 12 10 And 15
May 10, 2025
-
Which Of The Following Is Not Considered A Fossil Fuel
May 10, 2025
-
Naphthalene Balls Disappear With Time Without Leaving Any Solid
May 10, 2025
-
What Multiplies To 6 And Adds To 3
May 10, 2025
Related Post
Thank you for visiting our website which covers about Which Is More .25 Or .5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.