Which Is More 2 3 Or 3 4
Juapaving
May 13, 2025 · 5 min read
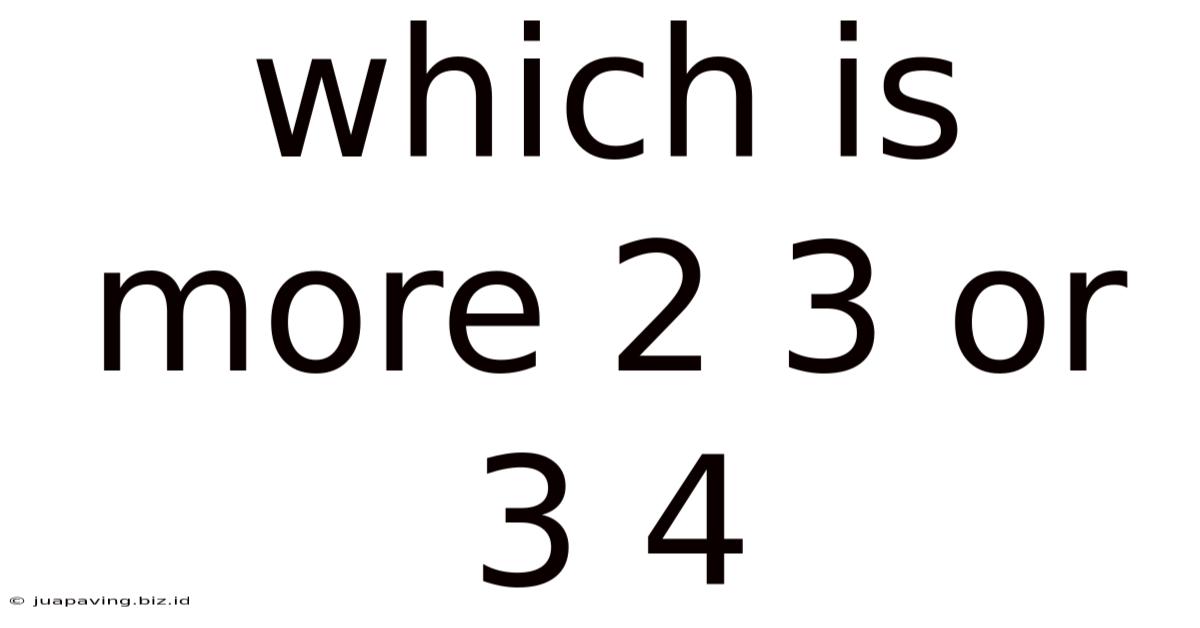
Table of Contents
Which is More: 2/3 or 3/4? A Deep Dive into Fractions and Comparative Analysis
Determining which fraction is larger, 2/3 or 3/4, might seem like a simple task, especially for those well-versed in mathematics. However, understanding the underlying principles and exploring various methods for comparison offers a valuable opportunity to solidify fractional comprehension and enhance mathematical reasoning skills. This article will explore multiple approaches to this problem, emphasizing the importance of conceptual understanding alongside procedural fluency. We'll delve into the nuances of fractions, comparing different techniques and highlighting their relative strengths and weaknesses.
Understanding Fractions: A Foundational Overview
Before directly comparing 2/3 and 3/4, let's refresh our understanding of fractions. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
For instance, in the fraction 2/3, the numerator is 2 and the denominator is 3. This signifies that we have 2 parts out of a total of 3 equal parts. Similarly, 3/4 represents 3 parts out of 4 equal parts.
Method 1: Finding a Common Denominator
This is arguably the most common and straightforward method for comparing fractions. The core idea is to rewrite both fractions with the same denominator. This allows for a direct comparison of the numerators.
To find a common denominator for 2/3 and 3/4, we need to identify a number that is divisible by both 3 and 4. The least common multiple (LCM) of 3 and 4 is 12.
-
Converting 2/3: To change the denominator from 3 to 12, we multiply both the numerator and the denominator by 4: (2 x 4) / (3 x 4) = 8/12
-
Converting 3/4: To change the denominator from 4 to 12, we multiply both the numerator and the denominator by 3: (3 x 3) / (4 x 3) = 9/12
Now we can easily compare: 8/12 and 9/12. Since 9 > 8, we conclude that 3/4 > 2/3.
Method 2: Converting to Decimals
Another effective way to compare fractions is to convert them into decimal equivalents. This method is particularly helpful when dealing with more complex fractions or when a numerical comparison is preferred.
-
Converting 2/3 to a decimal: 2 ÷ 3 ≈ 0.6667
-
Converting 3/4 to a decimal: 3 ÷ 4 = 0.75
Comparing the decimal equivalents, 0.75 > 0.6667, confirming that 3/4 > 2/3. This method provides a clear numerical representation, making the comparison readily apparent. Note that the decimal representation of 2/3 is a recurring decimal, meaning it continues infinitely. For practical purposes, we round it to a sufficient number of decimal places.
Method 3: Visual Representation
For a more intuitive understanding, especially for those who are visual learners, we can use visual aids such as diagrams or pie charts.
Imagine two identical circles.
-
Representing 2/3: Divide the first circle into three equal parts and shade two of them.
-
Representing 3/4: Divide the second circle into four equal parts and shade three of them.
By visually comparing the shaded areas, it becomes clear that the shaded area in the second circle (representing 3/4) is larger than the shaded area in the first circle (representing 2/3). This visual approach reinforces the conclusion that 3/4 > 2/3.
Method 4: Cross-Multiplication
This method provides a concise algebraic approach to comparing fractions. Cross-multiply the numerators and denominators of the two fractions. The fraction with the larger product is the larger fraction.
-
Cross-multiplying 2/3 and 3/4:
- (2 x 4) = 8
- (3 x 3) = 9
Since 9 > 8, we conclude that 3/4 > 2/3. This method offers an efficient way to compare fractions without the need for finding a common denominator or converting to decimals.
Expanding the Understanding: Applications and Further Exploration
The comparison of 2/3 and 3/4 provides a foundational stepping stone to understanding more complex fractional concepts. These skills are fundamental across various mathematical disciplines and practical applications.
-
Real-world applications: Imagine you're comparing two discounts: one offering a 2/3 reduction and another offering a 3/4 reduction. Understanding which fraction is larger directly impacts your choice, allowing for informed decision-making.
-
Advanced mathematics: The principles involved in comparing fractions are crucial in algebra, calculus, and other higher-level mathematical fields.
-
Developing number sense: Mastering fractional comparisons enhances number sense, improving one's ability to estimate, approximate, and reason quantitatively.
Addressing Common Errors and Misconceptions
While the comparison of 2/3 and 3/4 might seem straightforward, certain misconceptions can lead to incorrect conclusions. It's crucial to avoid the following:
-
Focusing solely on numerators or denominators: Simply observing that 3 > 2 and 4 > 3 is insufficient. The relative sizes of the numerators and denominators must be considered holistically.
-
Incorrect application of cross-multiplication: Ensure you multiply correctly and interpret the resulting products accurately.
-
Failing to simplify fractions: Before comparing fractions, simplify them to their lowest terms. This reduces complexity and minimizes errors.
Conclusion: Mastering Fractions for Enhanced Mathematical Proficiency
Comparing 2/3 and 3/4 reinforces the importance of mastering foundational fraction concepts. Through the exploration of various methods – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – we've established unequivocally that 3/4 is greater than 2/3. This understanding extends beyond simple comparisons, fostering a deeper appreciation for fractional arithmetic and its broader applications in mathematics and real-world problem-solving. By understanding these methods and avoiding common pitfalls, you can build confidence and proficiency in working with fractions. Continue practicing these techniques to develop strong mathematical intuition and skills. The seemingly simple act of comparing fractions underpins a wide array of more complex mathematical operations, making it a cornerstone of mathematical understanding.
Latest Posts
Latest Posts
-
What Is 36 Inches In Cm
May 13, 2025
-
The Nucleus Contains Protons And Responses
May 13, 2025
-
Does Translation Occur In The Cytoplasm
May 13, 2025
-
Find The Lowest Common Multiple Of 3 And 4
May 13, 2025
-
What Is The Fraction Of 37
May 13, 2025
Related Post
Thank you for visiting our website which covers about Which Is More 2 3 Or 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.