Which Is Larger 3/16 Or 1/4
Juapaving
May 09, 2025 · 5 min read
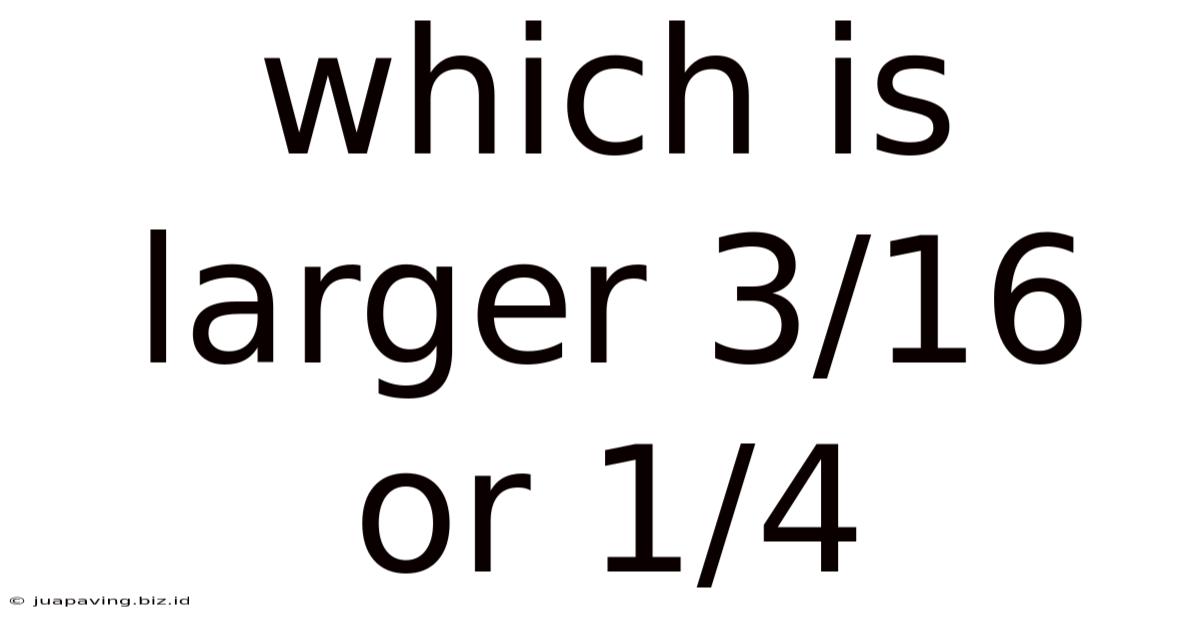
Table of Contents
Which is Larger: 3/16 or 1/4? A Deep Dive into Fraction Comparison
Understanding fractions is fundamental to mathematics and numerous real-world applications. While seemingly simple, comparing fractions like 3/16 and 1/4 can be challenging for some. This comprehensive guide will not only answer the question of which fraction is larger but also delve into the various methods for comparing fractions, providing you with a robust understanding of this essential mathematical concept.
Understanding Fractions: A Quick Refresher
Before we embark on comparing 3/16 and 1/4, let's revisit the basics of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number indicates how many equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) represents the number of parts we possess, and the denominator (4) represents the total number of equal parts the whole is divided into. Understanding this fundamental structure is crucial for comparing fractions effectively.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. Once they have the same denominator, we can directly compare their numerators.
Let's apply this method to compare 3/16 and 1/4:
-
Identify the denominators: The denominators are 16 and 4.
-
Find the least common multiple (LCM): The LCM of 16 and 4 is 16. This means we'll convert both fractions to have a denominator of 16.
-
Convert the fractions:
-
3/16 already has a denominator of 16, so it remains unchanged.
-
To convert 1/4 to a fraction with a denominator of 16, we multiply both the numerator and the denominator by 4: (1 * 4) / (4 * 4) = 4/16.
-
-
Compare the numerators: Now we compare 3/16 and 4/16. Since 4 > 3, we conclude that 4/16 (or 1/4) is larger than 3/16.
Method 2: Converting to Decimals
Another effective method for comparing fractions is to convert them into decimals. This approach is particularly useful when dealing with fractions that are difficult to compare using a common denominator.
To convert a fraction to a decimal, simply divide the numerator by the denominator.
Let's apply this method:
-
Convert 3/16 to a decimal: 3 ÷ 16 = 0.1875
-
Convert 1/4 to a decimal: 1 ÷ 4 = 0.25
-
Compare the decimals: Since 0.25 > 0.1875, we conclude that 1/4 is larger than 3/16.
Method 3: Visual Representation
Visual aids, like pie charts or number lines, can be extremely helpful in understanding and comparing fractions, especially for those who are visually oriented learners.
Imagine two circles, both divided into equal parts:
-
Circle 1: Divided into 16 equal parts, with 3 parts shaded. This represents 3/16.
-
Circle 2: Divided into 4 equal parts, with 1 part shaded. This represents 1/4.
By visually comparing the shaded areas, it becomes clear that the shaded area in Circle 2 (1/4) is larger than the shaded area in Circle 1 (3/16).
Practical Applications: Where Fraction Comparison Matters
Understanding fraction comparison isn't just an academic exercise; it has wide-ranging practical applications in various fields:
-
Cooking and Baking: Recipes often require precise measurements, making fraction comparison essential for accurate results. For example, determining whether 1/2 cup or 3/8 cup is a larger quantity is crucial for successful baking.
-
Construction and Engineering: Precise measurements are paramount in construction and engineering. Comparing fractions is crucial for ensuring accuracy in designs, blueprints, and measurements.
-
Finance: Fraction comparison plays a vital role in understanding interest rates, stock prices, and other financial calculations.
-
Data Analysis: In data analysis, fractions are frequently used to represent proportions and percentages. The ability to compare fractions accurately is critical for drawing meaningful conclusions from data.
-
Everyday Life: From dividing a pizza among friends to understanding discounts and sales, fraction comparison is frequently encountered in daily life.
Beyond the Basics: Working with Mixed Numbers and Improper Fractions
While this article focuses primarily on comparing simple fractions, it's important to acknowledge that fractions can also be expressed as mixed numbers (a whole number and a fraction) or improper fractions (where the numerator is larger than the denominator). To compare these, you'll first need to convert them to either improper fractions or decimals, then apply the methods discussed above. For example, to compare 1 1/2 and 7/4, you could convert them to improper fractions (3/2 and 7/4) and then find a common denominator or convert them to decimals (1.5 and 1.75).
Mastering Fraction Comparison: Tips and Tricks
Here are some helpful tips and tricks to enhance your fraction comparison skills:
-
Memorize common fraction equivalents: Knowing common equivalents like 1/2 = 2/4 = 4/8 can significantly speed up the comparison process.
-
Practice regularly: The more you practice comparing fractions, the more comfortable and efficient you will become.
-
Use visual aids: Don't underestimate the power of visual aids like pie charts or number lines in understanding and comparing fractions.
-
Check your work: Always double-check your calculations to ensure accuracy.
Conclusion: A Foundation for Future Mathematical Success
The ability to confidently compare fractions is a critical building block in mathematics. This skill forms the foundation for understanding more advanced concepts like ratios, proportions, and percentages. By mastering the methods and strategies outlined in this guide, you will not only be able to answer the question, "Which is larger: 3/16 or 1/4?" but also confidently tackle any fraction comparison problem you encounter. Remember to practice regularly and leverage various methods to reinforce your understanding and build a strong mathematical foundation. This knowledge will serve you well in your academic pursuits and various aspects of your daily life.
Latest Posts
Latest Posts
-
Solve Each System By Elimination Solver
May 10, 2025
-
What Is The Unit Of Measurement For Voltage
May 10, 2025
-
How Many Ft Is 33 Inches
May 10, 2025
-
Made Up Of More Than One Cell
May 10, 2025
-
Simplify The Square Root Of 343
May 10, 2025
Related Post
Thank you for visiting our website which covers about Which Is Larger 3/16 Or 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.