Which Is Greater 1 4 Or 1 8
Juapaving
May 13, 2025 · 4 min read
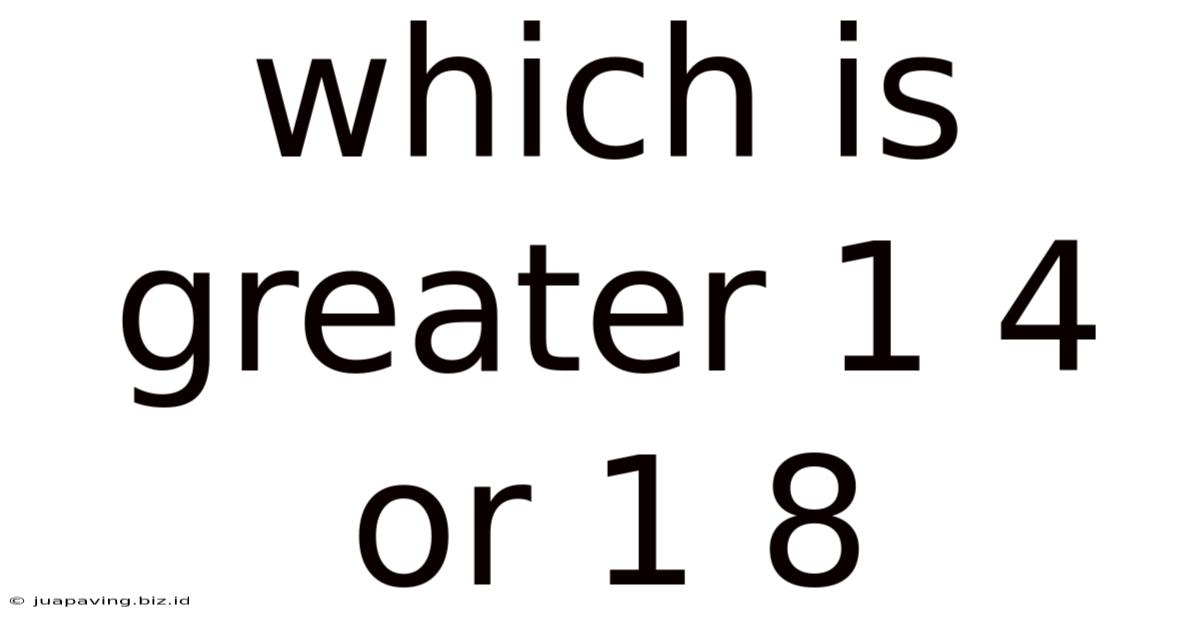
Table of Contents
Which is Greater: 1/4 or 1/8? A Deep Dive into Fractions
Understanding fractions is fundamental to mathematics and forms the basis for more advanced concepts. While the question, "Which is greater: 1/4 or 1/8?" might seem simple at first glance, it presents a valuable opportunity to explore the core principles of fractions, their representation, and comparison methods. This detailed guide will not only answer this question definitively but also delve into the underlying reasoning, providing you with a strong foundation for working with fractions in various contexts.
Understanding Fractions: A Foundational Overview
A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we are considering.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 1/4, the numerator (1) represents one part, and the denominator (4) signifies that the whole has been divided into four equal parts. Similarly, in 1/8, we have one part out of a whole divided into eight equal parts.
Visualizing Fractions: The Power of Representation
Visual aids are incredibly helpful in understanding fractions. Imagine a pizza cut into four equal slices (1/4). Now, imagine the same pizza cut into eight equal slices (1/8). If you take one slice from the pizza cut into four slices (1/4), you have a larger piece compared to taking one slice from the pizza cut into eight slices (1/8). This visual representation clearly demonstrates that 1/4 is greater than 1/8.
Comparing Fractions: Methods and Techniques
Several methods can be used to compare fractions. Let's explore the most common approaches:
Method 1: Common Denominator
This is perhaps the most straightforward method. To compare fractions, we find a common denominator – a number that is a multiple of both denominators. In our case, we have 1/4 and 1/8. The least common multiple (LCM) of 4 and 8 is 8. We then rewrite both fractions with the common denominator:
- 1/4 = (1 x 2) / (4 x 2) = 2/8
- 1/8 remains 1/8
Now, comparing 2/8 and 1/8, it’s evident that 2/8 (which is equivalent to 1/4) is greater than 1/8.
Method 2: Cross-Multiplication
This method provides an alternative approach to comparing fractions. We cross-multiply the numerators and denominators:
- (1/4) vs (1/8)
- 1 x 8 = 8
- 1 x 4 = 4
Since 8 > 4, the fraction 1/4 is greater than 1/8.
Method 3: Decimal Conversion
Converting fractions to decimals can also facilitate comparison.
- 1/4 = 0.25
- 1/8 = 0.125
Clearly, 0.25 > 0.125, confirming that 1/4 is greater than 1/8.
Understanding the Relationship: Proportions and Ratios
The relationship between 1/4 and 1/8 can also be understood in terms of proportions and ratios. 1/4 represents a larger proportion of a whole compared to 1/8. The ratio of 1/4 to 1/8 is 2:1, further emphasizing that 1/4 is twice as large as 1/8.
Real-World Applications: Putting Fractions to Use
Understanding the difference between 1/4 and 1/8 has numerous real-world applications:
Cooking and Baking:
Recipes often involve fractions. Knowing whether 1/4 cup of sugar is more or less than 1/8 cup is crucial for accurate measurements and successful baking.
Construction and Measurement:
In construction and other trades, precise measurements are paramount. Understanding fractional measurements is essential for accurate cutting, fitting, and building.
Finance and Budgeting:
Fractions are frequently used in finance and budgeting. Understanding proportions and ratios involving fractions helps in managing personal finances, analyzing investments, and understanding financial reports.
Data Analysis and Statistics:
Fractions are commonly used in data analysis and statistics to represent proportions and percentages. Understanding these concepts is crucial for interpreting data and drawing meaningful conclusions.
Beyond the Basics: Expanding Your Fractional Knowledge
While this article primarily focuses on comparing 1/4 and 1/8, it provides a strong foundation for working with fractions in general. To further enhance your understanding, consider exploring the following:
- Improper Fractions: Fractions where the numerator is greater than or equal to the denominator.
- Mixed Numbers: Numbers consisting of a whole number and a proper fraction.
- Fraction Operations: Addition, subtraction, multiplication, and division of fractions.
- Equivalent Fractions: Fractions that represent the same value, even though they have different numerators and denominators.
Conclusion: Mastering Fractions for Success
The question of which is greater, 1/4 or 1/8, might appear elementary, but its answer underpins a broader understanding of fractions, a fundamental concept in mathematics and numerous real-world applications. By grasping the methods for comparing fractions, whether through finding common denominators, cross-multiplication, or decimal conversion, you equip yourself with the tools needed to confidently approach and solve a wide range of mathematical problems. The more you practice and explore different aspects of fractions, the greater your understanding will become, ultimately leading to greater proficiency in mathematics and problem-solving skills in various aspects of life. So, remember that 1/4 is indeed greater than 1/8 – and armed with this understanding, you're well on your way to mastering fractions!
Latest Posts
Latest Posts
-
Which Of The Following Statements About Social Responsibility Is True
May 13, 2025
-
Why Are Coal Petroleum And Natural Gas Called Fossil Fuels
May 13, 2025
-
Does Prokaryotic Cells Have Golgi Apparatus
May 13, 2025
-
What Is 15 2 As A Decimal
May 13, 2025
-
Is Gold A Compound Or A Mixture
May 13, 2025
Related Post
Thank you for visiting our website which covers about Which Is Greater 1 4 Or 1 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.