Which Is Bigger 2 5 Or 1 3
Juapaving
Mar 24, 2025 · 5 min read
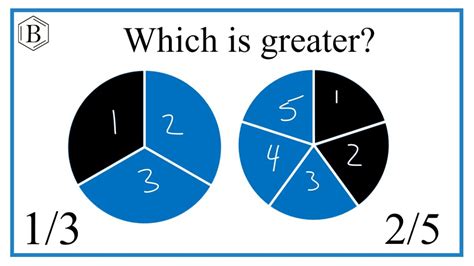
Table of Contents
Which is Bigger: 2/5 or 1/3? A Deep Dive into Fraction Comparison
Determining which fraction is larger, 2/5 or 1/3, might seem trivial at first glance. However, understanding the underlying principles of fraction comparison is crucial for a strong foundation in mathematics and problem-solving. This article will delve into several methods for comparing these fractions, explaining the logic behind each approach and providing practical examples to solidify your understanding. We'll go beyond a simple answer and explore the broader context of fractional arithmetic.
Understanding Fractions
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating how many equal parts the whole is divided into.
For instance, in the fraction 2/5, the numerator (2) represents two parts, and the denominator (5) means the whole is divided into five equal parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is finding a common denominator. This involves converting both fractions so they share the same denominator. Once they have the same denominator, we can directly compare their numerators.
Steps:
-
Find the Least Common Multiple (LCM): Determine the LCM of the denominators (5 and 3). The LCM is the smallest number that both 5 and 3 divide into evenly. In this case, the LCM of 5 and 3 is 15.
-
Convert the Fractions: Convert each fraction to an equivalent fraction with a denominator of 15.
- For 2/5: Multiply both the numerator and the denominator by 3: (2 x 3) / (5 x 3) = 6/15
- For 1/3: Multiply both the numerator and the denominator by 5: (1 x 5) / (3 x 5) = 5/15
-
Compare the Numerators: Now that both fractions have the same denominator, compare their numerators. Since 6 > 5, we conclude that 6/15 > 5/15.
Conclusion: Therefore, 2/5 (which is equivalent to 6/15) is bigger than 1/3 (which is equivalent to 5/15).
Method 2: Converting to Decimals
Another effective way to compare fractions is by converting them into decimal numbers. This method is particularly useful when dealing with more complex fractions or when you need a numerical value for further calculations.
Steps:
-
Divide the Numerator by the Denominator: For each fraction, divide the numerator by the denominator.
- 2/5 = 2 ÷ 5 = 0.4
- 1/3 = 1 ÷ 3 ≈ 0.333... (This is a repeating decimal)
-
Compare the Decimal Values: Compare the resulting decimal values. Since 0.4 > 0.333..., we can conclude that 2/5 is larger than 1/3.
Conclusion: Again, we find that 2/5 is bigger than 1/3.
Method 3: Visual Representation
Visualizing fractions using diagrams or models can be incredibly helpful, especially for beginners. This method provides an intuitive understanding of the comparison.
Imagine two identical bars representing the whole.
- For 2/5: Divide one bar into 5 equal parts and shade 2 of them.
- For 1/3: Divide the other bar into 3 equal parts and shade 1 of them.
By visually comparing the shaded portions, you'll clearly see that the shaded area representing 2/5 is larger than the shaded area representing 1/3.
Conclusion: The visual representation confirms that 2/5 is bigger than 1/3.
Expanding the Understanding: Beyond 2/5 and 1/3
While we've focused on comparing 2/5 and 1/3, the methods discussed can be applied to any pair of fractions. Let's consider some examples:
Example 1: Comparing 3/4 and 5/6
Using the common denominator method:
- LCM of 4 and 6 is 12
- 3/4 = 9/12
- 5/6 = 10/12
- Therefore, 5/6 > 3/4
Example 2: Comparing 7/8 and 2/3
Using the decimal method:
- 7/8 = 0.875
- 2/3 ≈ 0.666...
- Therefore, 7/8 > 2/3
Practical Applications: Where Fraction Comparison Matters
The ability to compare fractions is fundamental to many areas, including:
- Baking and Cooking: Following recipes often requires understanding and adjusting ingredient ratios, which involves comparing fractions.
- Construction and Engineering: Precise measurements and calculations in construction rely heavily on fraction manipulation and comparison.
- Finance: Calculating percentages, interest rates, and proportions all involve working with fractions.
- Data Analysis: Understanding data often necessitates comparing fractions to interpret proportions and trends.
Mastering Fraction Comparison: Tips and Tricks
- Practice Regularly: The more you practice comparing fractions, the more comfortable and efficient you'll become.
- Choose the Easiest Method: Select the method that feels most intuitive and efficient for you. Some methods might be better suited for certain types of fractions.
- Use Visual Aids: Diagrams and models can be incredibly helpful, particularly when starting out.
- Understand the Logic: Don't just memorize steps; understand the underlying principles behind each method.
Conclusion: A Solid Foundation for Future Math Success
Comparing fractions, such as determining whether 2/5 or 1/3 is larger, is a seemingly simple task that underpins a more profound understanding of mathematical concepts. By mastering various methods for fraction comparison—finding a common denominator, converting to decimals, or utilizing visual representations—you build a strong foundation for success in more advanced mathematical endeavors. The ability to confidently compare fractions extends far beyond the classroom, proving valuable in numerous practical applications throughout life. Through consistent practice and a solid grasp of the underlying principles, you can unlock the power of fractions and confidently tackle any fraction comparison challenge.
Latest Posts
Latest Posts
-
Vidhan Sabha Vs Lok Sabha Vs Rajya Sabha
Mar 29, 2025
-
What Can 81 Be Divided By
Mar 29, 2025
-
A Number Is Divisible By 6 If
Mar 29, 2025
-
What Stores Water In Plant Cells
Mar 29, 2025
-
Exercise On Transitive And Intransitive Verbs
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Which Is Bigger 2 5 Or 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
