Which Is Bigger 1 2 Or 2 3
Juapaving
May 10, 2025 · 5 min read
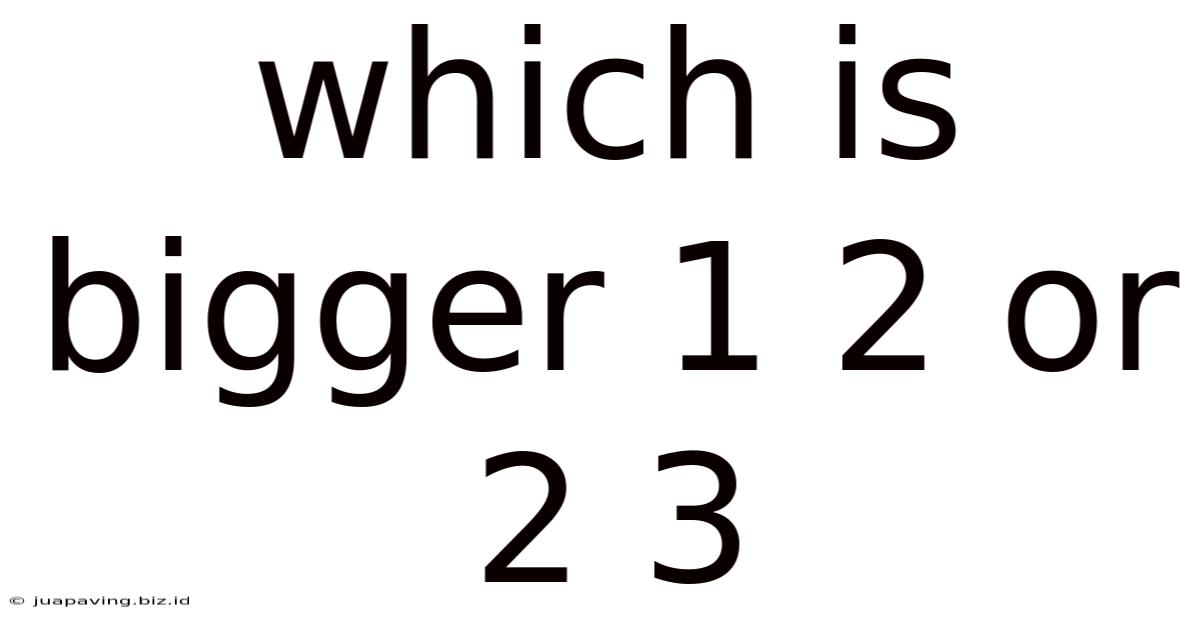
Table of Contents
Which is Bigger: 1/2 or 2/3? A Deep Dive into Fraction Comparison
Determining which fraction is larger, 1/2 or 2/3, might seem trivial at first glance. However, a deeper exploration reveals valuable insights into fundamental mathematical concepts and provides a fertile ground for illustrating various comparison techniques. This comprehensive guide will not only answer the question definitively but also equip you with the skills to compare any two fractions effectively.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's revisit the basics of fractions. A fraction represents a part of a whole. It's composed of two essential parts:
- Numerator: The top number indicates the number of parts considered.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) signifies one part, while the denominator (2) indicates the whole is divided into two equal parts. Similarly, 2/3 represents two parts out of a total of three equal parts.
Method 1: Finding a Common Denominator
This is arguably the most common and straightforward method for comparing fractions. The core idea is to rewrite both fractions so they share the same denominator. This allows for a direct comparison of the numerators.
To find a common denominator for 1/2 and 2/3, we need to find the least common multiple (LCM) of 2 and 3. The LCM is the smallest number that is a multiple of both 2 and 3. In this case, the LCM is 6.
Now, let's rewrite each fraction with a denominator of 6:
- 1/2: To change the denominator from 2 to 6, we multiply both the numerator and the denominator by 3: (1 * 3) / (2 * 3) = 3/6
- 2/3: To change the denominator from 3 to 6, we multiply both the numerator and the denominator by 2: (2 * 2) / (3 * 2) = 4/6
Now that both fractions have the same denominator (6), we can easily compare their numerators: 3 and 4. Since 4 > 3, we conclude that 2/3 > 1/2.
Method 2: Converting to Decimals
Another effective method involves converting the fractions into their decimal equivalents. This approach is particularly useful when dealing with fractions that are difficult to visualize or find a common denominator for.
Let's convert 1/2 and 2/3 into decimals:
- 1/2: 1 divided by 2 equals 0.5
- 2/3: 2 divided by 3 equals approximately 0.6667 (this is a repeating decimal)
Comparing the decimal values, we see that 0.6667 > 0.5. Therefore, 2/3 > 1/2.
Method 3: Visual Representation
Visual aids can greatly enhance understanding, especially when dealing with fractions. Imagine a circle divided into equal parts.
For 1/2, imagine a circle cut into two equal halves. Shading one half represents 1/2.
For 2/3, imagine a circle cut into three equal parts. Shading two of these parts represents 2/3.
By visually comparing the shaded areas, it's evident that the shaded area representing 2/3 is larger than the shaded area representing 1/2. Therefore, 2/3 > 1/2.
Method 4: Cross-Multiplication
This method offers a quick and efficient way to compare two fractions without finding a common denominator. Cross-multiplication involves multiplying the numerator of one fraction by the denominator of the other and vice-versa.
Let's compare 1/2 and 2/3 using cross-multiplication:
- Multiply the numerator of the first fraction (1) by the denominator of the second fraction (3): 1 * 3 = 3
- Multiply the numerator of the second fraction (2) by the denominator of the first fraction (2): 2 * 2 = 4
Compare the results: 3 < 4. Since the result of the second multiplication (4) is greater, the second fraction (2/3) is larger. Therefore, 2/3 > 1/2.
Beyond the Basics: Extending Fraction Comparison Skills
The methods outlined above provide a solid foundation for comparing fractions. However, mastering fraction comparison requires practice and an understanding of several key concepts:
- Improper Fractions and Mixed Numbers: Learn to convert improper fractions (where the numerator is larger than the denominator) to mixed numbers (a combination of a whole number and a fraction) for easier comparison. For example, 7/4 can be converted to 1 ¾.
- Equivalent Fractions: Recognize that fractions can represent the same value even if they look different. For example, 1/2, 2/4, and 3/6 are all equivalent fractions.
- Comparing More Than Two Fractions: When comparing more than two fractions, the common denominator method remains the most reliable approach. Find the LCM of all the denominators and rewrite all fractions with that common denominator.
Practical Applications of Fraction Comparison
The ability to compare fractions is not merely an academic exercise. It has practical applications in various fields:
- Cooking and Baking: Following recipes often involves accurately measuring ingredients, which necessitates understanding fraction comparisons.
- Construction and Engineering: Precision in measurements is paramount in these fields, and comparing fractions is crucial for ensuring accuracy.
- Finance and Accounting: Working with percentages and proportions, often expressed as fractions, is commonplace in financial calculations.
- Data Analysis: When analyzing data represented in fractions or proportions, the ability to compare them effectively is essential for drawing accurate conclusions.
Conclusion: Mastering Fraction Comparison for Enhanced Mathematical Proficiency
Determining whether 1/2 or 2/3 is bigger is a stepping stone to a deeper understanding of fractions and their comparison. The methods outlined – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – provide a versatile toolkit for tackling fraction comparison problems of varying complexity. By mastering these techniques and understanding the underlying concepts, you'll enhance your mathematical proficiency and confidently handle fraction-related tasks in various real-world scenarios. Remember to practice regularly to solidify your skills and build confidence in your mathematical abilities. The more you practice, the easier and faster these comparisons will become. And don't be afraid to use multiple methods to check your work; it's a valuable way to reinforce understanding and catch potential errors.
Latest Posts
Latest Posts
-
How Many Minutes Is 140 Seconds
May 10, 2025
-
Addition Of Integers On Number Line
May 10, 2025
-
Distinguish Between Infrasonic And Ultrasonic Sound Waves
May 10, 2025
-
What Are The Three Parts Of The Seed
May 10, 2025
-
What Is The Molar Mass Of Nh4no3
May 10, 2025
Related Post
Thank you for visiting our website which covers about Which Is Bigger 1 2 Or 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.