Which Expression Is Equivalent To 5 2 5 1
Juapaving
May 12, 2025 · 4 min read
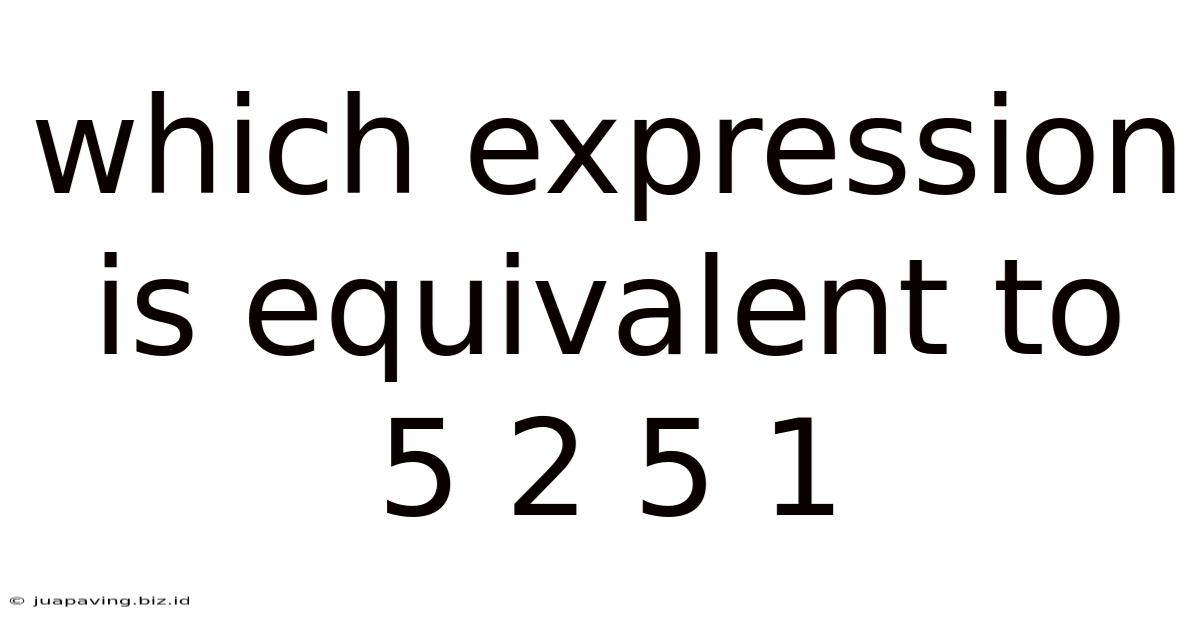
Table of Contents
Which Expression is Equivalent to 5²⁵¹? Unlocking the Mystery of Mathematical Equivalence
The question, "Which expression is equivalent to 5²⁵¹?", might seem deceptively simple at first glance. However, understanding its nuances requires a deep dive into the world of mathematical notation, specifically focusing on exponents and their properties. This article will not only answer this question but also explore the underlying principles of exponential expressions, providing you with a solid foundation for tackling similar problems.
Understanding Exponential Notation
Before we delve into finding equivalent expressions for 5²⁵¹, let's solidify our understanding of exponential notation. An expression like 5²⁵¹ represents a power, where:
- 5 is the base: This is the number being multiplied repeatedly.
- 251 is the exponent: This indicates how many times the base is multiplied by itself.
Therefore, 5²⁵¹ means 5 multiplied by itself 251 times: 5 x 5 x 5 x ... x 5 (251 times).
Calculating this directly is computationally intensive, even for powerful computers. This is where the importance of finding equivalent expressions comes into play. Equivalent expressions simplify calculations and offer alternative representations of the same numerical value.
Exploring Potential Equivalent Expressions
Finding an expression equivalent to 5²⁵¹ requires exploring various mathematical properties and manipulations. Unfortunately, there isn't a single, simple equivalent expression that significantly reduces the computational burden. The sheer magnitude of the exponent (251) makes direct simplification challenging. However, we can explore several avenues to represent the expression differently:
1. Prime Factorization: A Foundation for Simplification
While direct simplification isn't feasible, we can analyze the base (5) through prime factorization. Since 5 is itself a prime number (a number divisible only by 1 and itself), prime factorization doesn't offer further simplification in this specific case. However, if the base were a composite number (a number with more than two factors), prime factorization could be a powerful tool for simplification. For example, if the expression were 10²⁵¹, we could factor 10 as 2 x 5, leading to (2 x 5)²⁵¹, which could then be further manipulated using exponential rules.
2. Utilizing Exponential Rules: The Key to Manipulation
Exponential rules provide the most potent tools for manipulating and potentially simplifying exponential expressions. Let's review some key rules:
- Product of Powers: aᵐ x aⁿ = aᵐ⁺ⁿ (When multiplying powers with the same base, add the exponents.)
- Quotient of Powers: aᵐ / aⁿ = aᵐ⁻ⁿ (When dividing powers with the same base, subtract the exponents.)
- Power of a Power: (aᵐ)ⁿ = aᵐⁿ (When raising a power to another power, multiply the exponents.)
- Power of a Product: (ab)ⁿ = aⁿbⁿ (The power applies to each factor in the product.)
- Power of a Quotient: (a/b)ⁿ = aⁿ/bⁿ (The power applies to both the numerator and the denominator.)
Applying these rules to 5²⁵¹ directly doesn't immediately lead to a simpler expression because the base is a prime number and the exponent is already in its simplest form.
3. Logarithmic Representation: An Alternative Perspective
Logarithms provide an alternative way to represent exponential expressions. The logarithmic form of an exponential expression aˣ = y is logₐy = x. Therefore, we can represent 5²⁵¹ using logarithms:
log₅(y) = 251, where y = 5²⁵¹
This representation doesn't simplify the calculation directly, but it provides a different perspective and is useful in certain mathematical contexts, especially when dealing with equations involving exponents. For instance, solving equations that involve variables in the exponents often requires the use of logarithms.
4. Approximations: Handling Immense Numbers
Given the immense size of 5²⁵¹, we might consider using approximations. However, even logarithmic approximations will yield a very large number. While we can't find an exactly equivalent simplified expression, approximating its magnitude using logarithms can be helpful for understanding its scale. A scientific calculator or programming language would be necessary for this type of calculation.
The Importance of Context: Why Equivalent Expressions Matter
The search for an equivalent expression to 5²⁵¹ highlights the importance of considering the context of the problem. While a dramatically simplified equivalent expression might not exist in this specific case, the principles explored—prime factorization and exponential rules—are crucial in various mathematical situations. Understanding these principles is key to:
- Simplifying Calculations: In many instances, applying exponential rules leads to significantly simpler calculations, saving time and effort.
- Solving Equations: Exponential rules and logarithms are essential for solving equations involving exponents.
- Understanding Growth and Decay: Exponential expressions are fundamental in modeling exponential growth and decay phenomena in various fields like finance, biology, and physics.
Conclusion: Embracing the Complexity
While we haven't found a dramatically simplified equivalent expression for 5²⁵¹, the journey of exploring potential approaches has highlighted the fundamental principles of exponential notation and the power of mathematical manipulation. This exploration underscores the importance of understanding exponential rules and the role of context in determining the most effective approach to working with exponential expressions. Remember that the absence of a simpler equivalent doesn't diminish the significance of the original expression; it simply highlights the vastness of the number it represents. The process of exploring potential solutions is just as valuable as finding a neat, simplified answer. It's this exploration that builds a stronger understanding of mathematical principles and enhances problem-solving skills. This pursuit of understanding is, in itself, the core of mathematical learning.
Latest Posts
Latest Posts
-
Five Letter Words That End With On
May 14, 2025
-
How Many Glass Is 1 Liter Of Water
May 14, 2025
-
Words That End With I N G
May 14, 2025
-
How Many Legs Does And Ant Have
May 14, 2025
-
What Is A Group Of Fish Called
May 14, 2025
Related Post
Thank you for visiting our website which covers about Which Expression Is Equivalent To 5 2 5 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.