Which Expression Is Equivalent To 24 1/3
Juapaving
May 11, 2025 · 5 min read
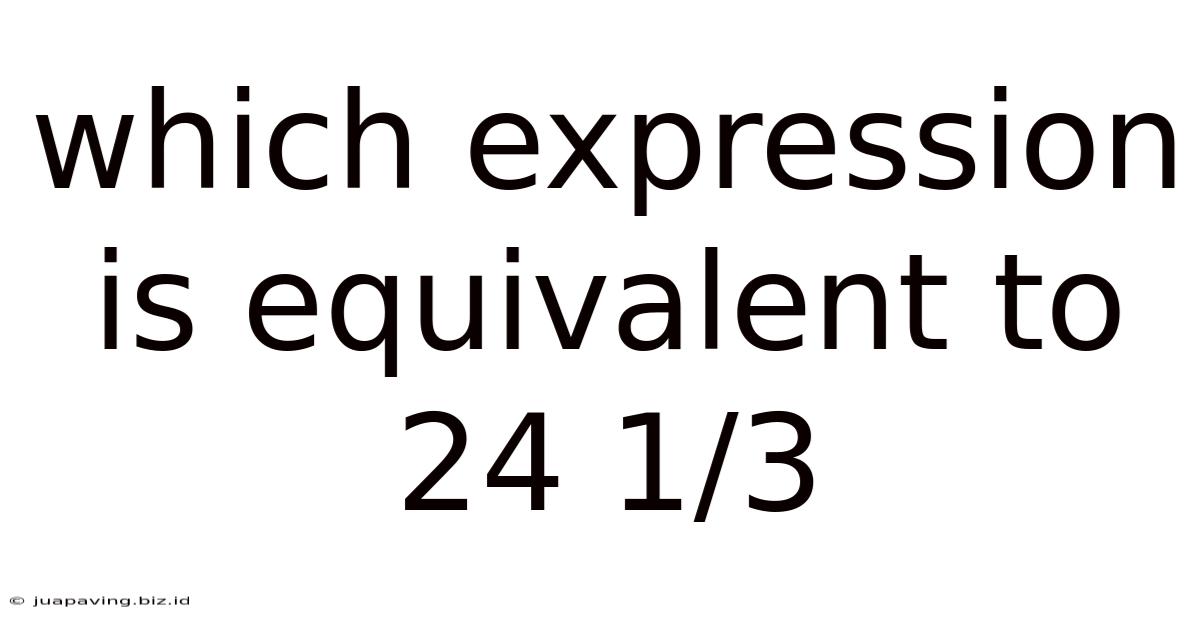
Table of Contents
Which Expression is Equivalent to 24 1/3? A Comprehensive Guide
Finding equivalent expressions is a fundamental skill in mathematics, crucial for simplifying calculations and solving equations. This article delves deep into the various ways to represent the mixed number 24 1/3, exploring different equivalent expressions, demonstrating the methods used, and highlighting the importance of understanding these equivalencies in various mathematical contexts.
Understanding Mixed Numbers and Improper Fractions
Before diving into equivalent expressions for 24 1/3, let's solidify our understanding of mixed numbers and improper fractions. A mixed number combines a whole number and a fraction, like 24 1/3. An improper fraction, on the other hand, has a numerator larger than or equal to its denominator. These two forms are interchangeable, making them essential for finding equivalent expressions.
Converting a Mixed Number to an Improper Fraction
To convert a mixed number to an improper fraction, follow these steps:
- Multiply the whole number by the denominator: 24 * 3 = 72
- Add the numerator: 72 + 1 = 73
- Keep the same denominator: The denominator remains 3.
Therefore, 24 1/3 is equivalent to the improper fraction 73/3.
Converting an Improper Fraction to a Mixed Number
The reverse process is equally important. To convert an improper fraction to a mixed number:
- Divide the numerator by the denominator: 73 ÷ 3 = 24 with a remainder of 1.
- The quotient becomes the whole number: 24
- The remainder becomes the numerator: 1
- The denominator remains the same: 3
This gives us the mixed number 24 1/3.
Equivalent Expressions for 24 1/3: A Multifaceted Approach
Now, let's explore a variety of expressions equivalent to 24 1/3, utilizing different mathematical operations and concepts.
1. Decimal Representation
Converting the mixed number or improper fraction to a decimal provides another equivalent expression. To do this, simply divide the numerator by the denominator:
73 ÷ 3 = 24.333...
This is a recurring decimal, often represented as 24.3̅3̅. It's important to understand that this decimal representation goes on infinitely. For practical purposes, rounding might be necessary, depending on the context of the problem.
2. Using Equivalent Fractions
Creating equivalent fractions offers a multitude of expressions equal to 24 1/3 or 73/3. To generate an equivalent fraction, multiply both the numerator and denominator by the same non-zero number.
For instance:
- Multiplying by 2: (73 * 2) / (3 * 2) = 146/6
- Multiplying by 3: (73 * 3) / (3 * 3) = 219/9
- Multiplying by 4: (73 * 4) / (3 * 4) = 292/12
This method allows for an infinite number of equivalent fractions.
3. Sum of Fractions
We can express 24 1/3 as a sum of fractions. One simple approach is to break down the whole number part:
24 1/3 = 24 + 1/3
Alternatively, we can express it as a sum of fractions with different denominators, finding common denominators as needed:
24 1/3 = 23 + 2/3 + 1/3 = 23 + 1 + 1/3 = 24 + 1/3. This demonstrates the flexibility in breaking down the number.
4. Difference of Fractions
Similar to the sum of fractions, we can represent 24 1/3 as the difference of two fractions. This requires creativity and finding suitable numerators and denominators. For example:
24 1/3 could be expressed as 74/3 - 1/3. This is a less intuitive approach than the sum of fractions but still shows equivalent expression possibilities.
5. Using Percentage
To express 24 1/3 as a percentage, convert the mixed number to a decimal (24.333...) and multiply by 100:
24.333... * 100 = 2433.333...% Again, the repeating decimal indicates an infinite representation.
The Importance of Equivalent Expressions
Understanding and utilizing equivalent expressions is paramount in mathematics for several reasons:
- Simplification: Converting to a simpler form, such as an improper fraction or decimal, often makes calculations easier.
- Problem Solving: Different expressions can provide different insights into a problem and help in finding solutions. The best way to approach the solution depends on the equation, inequality, or problem at hand.
- Comparison: Equivalent expressions are necessary for comparing quantities and determining which one is bigger or smaller.
- Generalization: The concept of equivalent expressions extends to more complex mathematical topics like algebra and calculus.
Practical Applications
The concept of equivalent expressions isn't confined to theoretical mathematics; it has widespread practical applications:
- Measurement: In construction or engineering, converting between fractions, decimals, and percentages is crucial for accurate measurements. For example, expressing a length as 24 1/3 feet might be more convenient than using its decimal equivalent in certain contexts.
- Finance: Calculations involving interest rates, profit margins, and tax often utilize decimals and percentages, requiring conversions from fractions for accurate calculation and easier comprehension.
- Cooking: Recipes often use fractional measurements, while adjusting those recipes requires understanding equivalent fractions for scaling up or down.
- Data Analysis: Data analysis frequently involves working with fractions and percentages, making the ability to express them in different forms a necessary skill.
Conclusion
The mixed number 24 1/3, as we've demonstrated, can be represented in numerous equivalent expressions, including improper fractions, decimals, percentages, sums, and differences of fractions. The ability to convert between these forms is a fundamental skill in mathematics, essential for simplifying calculations, solving problems, and interpreting results across various fields. Mastering the conversion between these forms is essential for success in mathematics and its practical applications. By understanding the methods outlined in this comprehensive guide, you'll be well-equipped to handle equivalent expressions with confidence and efficiency. Remember that the choice of representation often depends on the specific problem and the desired level of precision.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 10 And 20
May 12, 2025
-
What Is The Freezing Point Of Blood
May 12, 2025
-
In Celsius What Is The Freezing Point Of Water
May 12, 2025
-
Difference Between Internal And External Fertilisation
May 12, 2025
-
What Is The Length Of A Pencil In Cm
May 12, 2025
Related Post
Thank you for visiting our website which covers about Which Expression Is Equivalent To 24 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.