Which Equation Represents The Combined Gas Law
Juapaving
May 09, 2025 · 6 min read
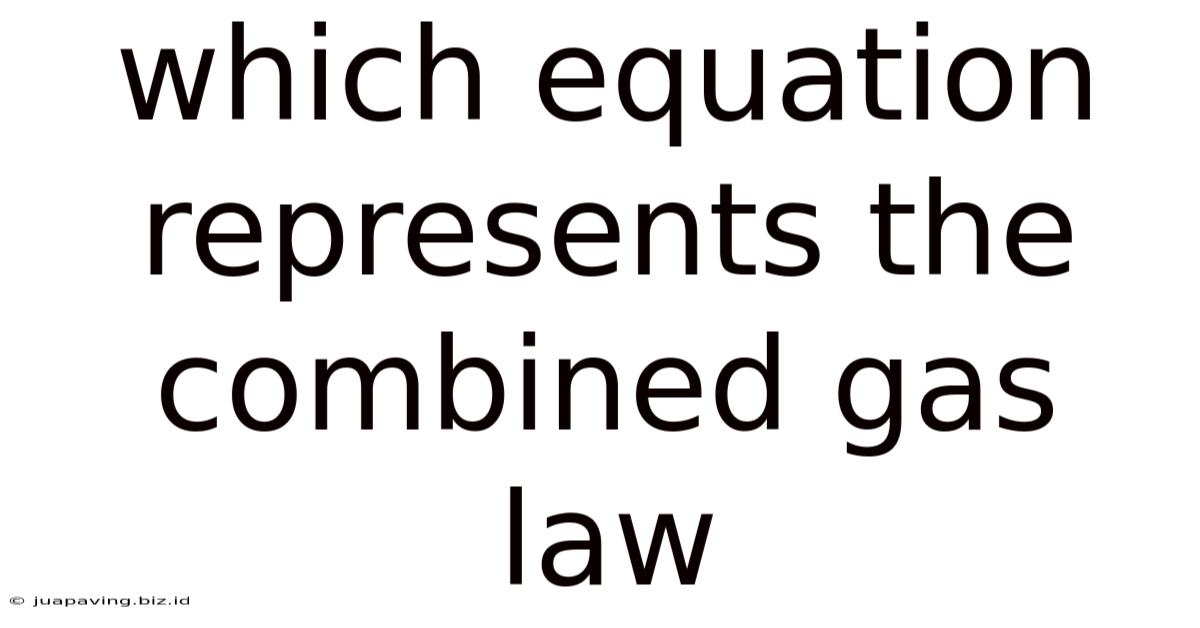
Table of Contents
Which Equation Represents the Combined Gas Law? A Comprehensive Guide
The combined gas law is a crucial concept in chemistry and physics, describing the relationship between pressure, volume, and temperature of a fixed amount of gas. Understanding this law and its underlying equation is vital for numerous applications, from understanding atmospheric phenomena to designing industrial processes. This comprehensive guide will delve deep into the combined gas law, exploring its equation, derivation, applications, and limitations. We'll also address common misconceptions and provide practical examples to solidify your understanding.
Understanding the Individual Gas Laws
Before diving into the combined gas law, let's review the three individual gas laws that form its foundation:
1. Boyle's Law: Pressure and Volume
Boyle's Law states that at a constant temperature, the volume of a gas is inversely proportional to its pressure. This means that if you increase the pressure on a gas, its volume will decrease proportionally, and vice versa. Mathematically, it's represented as:
P₁V₁ = P₂V₂
Where:
- P₁ = initial pressure
- V₁ = initial volume
- P₂ = final pressure
- V₂ = final volume
2. Charles's Law: Volume and Temperature
Charles's Law describes the relationship between the volume and temperature of a gas at constant pressure. It states that the volume of a gas is directly proportional to its absolute temperature (measured in Kelvin). As temperature increases, the volume increases proportionally, and vice versa. The equation is:
V₁/T₁ = V₂/T₂
Where:
- V₁ = initial volume
- T₁ = initial temperature (in Kelvin)
- V₂ = final volume
- T₂ = final temperature (in Kelvin)
3. Gay-Lussac's Law: Pressure and Temperature
Gay-Lussac's Law focuses on the relationship between pressure and temperature at constant volume. It states that the pressure of a gas is directly proportional to its absolute temperature. An increase in temperature leads to a proportional increase in pressure, and vice versa. The equation is:
P₁/T₁ = P₂/T₂
Where:
- P₁ = initial pressure
- T₁ = initial temperature (in Kelvin)
- P₂ = final pressure
- T₂ = final temperature (in Kelvin)
Deriving the Combined Gas Law Equation
The combined gas law elegantly combines Boyle's, Charles's, and Gay-Lussac's laws into a single equation that describes the relationship between pressure, volume, and temperature of a fixed amount of gas when all three variables change simultaneously.
By combining the individual gas laws, we arrive at the combined gas law equation:
P₁V₁/T₁ = P₂V₂/T₂
This equation shows that the ratio of the product of pressure and volume to the absolute temperature remains constant for a given amount of gas.
Understanding the Combined Gas Law Equation
The combined gas law equation, P₁V₁/T₁ = P₂V₂/T₂, is incredibly useful for solving problems where pressure, volume, and temperature of a gas change simultaneously. Let's break down each variable:
-
P₁ and P₂: Represent the initial and final pressures of the gas, respectively. Pressure is usually measured in atmospheres (atm), Pascals (Pa), or millimeters of mercury (mmHg).
-
V₁ and V₂: Represent the initial and final volumes of the gas, respectively. Volume is typically measured in liters (L) or cubic meters (m³).
-
T₁ and T₂: Represent the initial and final absolute temperatures of the gas, respectively. It is crucial to use the Kelvin scale (K) for temperature in the combined gas law. To convert Celsius (°C) to Kelvin (K), add 273.15: K = °C + 273.15.
Applications of the Combined Gas Law
The combined gas law has a wide range of applications in various fields:
-
Meteorology: Predicting weather patterns involves understanding how temperature, pressure, and volume of air masses change.
-
Automotive Engineering: Designing internal combustion engines relies on understanding how the pressure, volume, and temperature of gases change during the combustion cycle.
-
Aerospace Engineering: Calculating the lift generated by aircraft wings involves considering the changes in air pressure and temperature at different altitudes.
-
Industrial Processes: Many industrial processes involve gases, and the combined gas law is essential for designing and optimizing these processes. Examples include chemical reactions, gas storage, and transportation.
-
Scuba Diving: Understanding how pressure, volume, and temperature affect the gases in scuba tanks is critical for diver safety.
-
Weather Balloons: The expansion and contraction of weather balloons at different altitudes are directly related to the combined gas law.
Solving Problems Using the Combined Gas Law
To effectively use the combined gas law, follow these steps:
-
Identify the known variables: Determine the values of pressure (P), volume (V), and temperature (T) at both the initial and final states.
-
Convert units: Ensure all units are consistent. Commonly used units include atmospheres for pressure, liters for volume, and Kelvin for temperature.
-
Substitute values into the equation: Plug the known values into the combined gas law equation: P₁V₁/T₁ = P₂V₂/T₂
-
Solve for the unknown variable: Rearrange the equation to solve for the variable you need to find.
-
Check your answer: Ensure your answer is reasonable and makes physical sense in the context of the problem.
Example Problem
Let's say a gas occupies 5.0 L at 25°C and 1.0 atm. What volume will it occupy at 50°C and 1.5 atm?
-
Known Variables:
- P₁ = 1.0 atm
- V₁ = 5.0 L
- T₁ = 25°C + 273.15 = 298.15 K
- P₂ = 1.5 atm
- T₂ = 50°C + 273.15 = 323.15 K
- V₂ = ?
-
Equation: P₁V₁/T₁ = P₂V₂/T₂
-
Solve for V₂: Rearrange the equation to solve for V₂: V₂ = (P₁V₁T₂)/(T₁P₂)
-
Substitute and Calculate: V₂ = (1.0 atm * 5.0 L * 323.15 K) / (298.15 K * 1.5 atm) V₂ ≈ 3.4 L
Therefore, the gas will occupy approximately 3.4 L at 50°C and 1.5 atm.
Limitations of the Combined Gas Law
The combined gas law is an approximation, and it has certain limitations:
-
Ideal Gas Assumption: The combined gas law assumes that the gas behaves ideally. Real gases deviate from ideal behavior, especially at high pressures and low temperatures.
-
Constant Amount of Gas: The law applies only to a fixed amount of gas. If the amount of gas changes (e.g., gas is added or removed), the combined gas law is not applicable.
-
No Phase Changes: The law is only valid if the gas remains in the gaseous phase throughout the process. If a phase change (e.g., condensation or vaporization) occurs, the combined gas law cannot be used.
Conclusion
The combined gas law is a powerful tool for understanding and predicting the behavior of gases under changing conditions. Understanding its derivation, equation, applications, and limitations is essential for various scientific and engineering disciplines. By mastering this fundamental concept, you’ll gain valuable insights into the world of gases and their behavior in diverse scenarios. Remember always to convert temperatures to Kelvin and to consider the limitations of the ideal gas assumption when applying this law to real-world situations.
Latest Posts
Latest Posts
-
Units For Rate Constant K Third Order
May 09, 2025
-
What Is A Equivalent Fraction For 1 4
May 09, 2025
-
Which Element Has The Greatest Number Of Valence Electrons
May 09, 2025
-
Which Expression Is Not A Polynomial
May 09, 2025
-
Least Common Multiple Of 11 And 13
May 09, 2025
Related Post
Thank you for visiting our website which covers about Which Equation Represents The Combined Gas Law . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.