Which Algebraic Expressions Are Polynomials Check All That Apply
Juapaving
Apr 05, 2025 · 6 min read
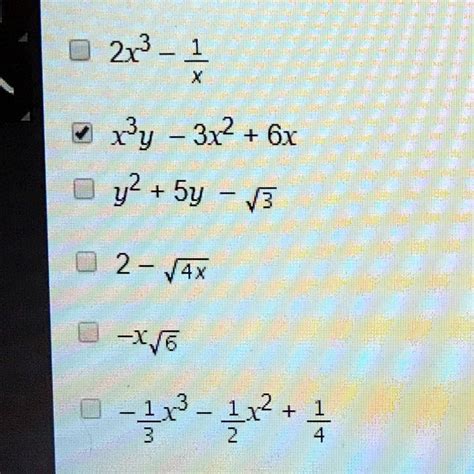
Table of Contents
Which Algebraic Expressions Are Polynomials? Check All That Apply
Understanding polynomials is fundamental in algebra and beyond. They form the bedrock for many advanced mathematical concepts and are frequently encountered in various fields like physics, engineering, and computer science. But what exactly is a polynomial, and how can you quickly identify one among a collection of algebraic expressions? This comprehensive guide will equip you with the knowledge to confidently distinguish polynomials from other algebraic expressions. We'll explore the defining characteristics of polynomials, common misconceptions, and provide numerous examples to solidify your understanding.
Defining a Polynomial: The Key Characteristics
A polynomial is a mathematical expression involving a sum of powers in one or more variables multiplied by coefficients. Let's break down the crucial elements:
-
Terms: A polynomial consists of one or more terms. Each term is a product of a constant (coefficient) and one or more variables raised to non-negative integer powers.
-
Coefficients: These are the numerical factors multiplying the variables in each term. They can be integers, rational numbers, real numbers, or even complex numbers, depending on the context.
-
Variables: These are the symbolic representations, often denoted by letters like x, y, z, etc.
-
Exponents: The powers to which the variables are raised must be non-negative integers (0, 1, 2, 3, and so on). This is a critical characteristic that distinguishes polynomials from other algebraic expressions.
In short: A polynomial is an expression of the form:
a_nx^n + a_{n-1}x^{n-1} + ... + a_2x^2 + a_1x + a_0
where:
a_n, a_{n-1}, ..., a_0are the coefficients (constants).nis a non-negative integer (the degree of the polynomial).xis the variable.
Identifying Polynomials: Examples and Non-Examples
Let's delve into examples to solidify the concept. We'll analyze several algebraic expressions, determining whether they are polynomials and justifying our answers.
Examples of Polynomials:
-
3x² + 2x - 5: This is a polynomial. It has three terms, all with non-negative integer exponents on the variable 'x'. The coefficients are 3, 2, and -5.
-
5y⁴ - 7y² + 2: A polynomial in the variable 'y'. Notice the exponents (4, 2, 0) are all non-negative integers.
-
-4z: This is a polynomial of degree 1 (a linear polynomial). It can be written as -4z¹ + 0.
-
7: This is a constant polynomial (degree 0). It can be considered a polynomial with a single term, 7x⁰, where x⁰ = 1.
-
2x³y² + 5xy - 3: This is a polynomial in two variables, x and y. All exponents (3, 2, 1, 0) are non-negative integers.
Non-Examples of Polynomials:
-
1/x + 2: This is not a polynomial because the term '1/x' can be written as x⁻¹, and the exponent -1 is a negative integer. Polynomials only allow for non-negative integer exponents.
-
√x + 5: This expression involves a square root of the variable, equivalent to x^(1/2). The exponent (1/2) is not an integer.
-
x⁻² + 3x + 1: This expression contains a negative exponent (-2), making it not a polynomial.
-
2ˣ + x²: This is not a polynomial because the variable 'x' appears as an exponent. Polynomials have variables only in the base, not in the exponent.
-
3/x² + 4x - 7: The term '3/x²' is equivalent to 3x⁻², which contains a negative exponent.
-
|x| + 2: The absolute value function, |x|, is not a polynomial function. Polynomial functions are continuous and smooth everywhere, while the absolute value function has a sharp corner at x = 0.
Understanding the Degree of a Polynomial
The degree of a polynomial is the highest power of the variable present in the expression. Let's look at some examples:
- 3x² + 2x - 5: Degree 2 (quadratic polynomial)
- 5y⁴ - 7y² + 2: Degree 4 (quartic polynomial)
- -4z: Degree 1 (linear polynomial)
- 7: Degree 0 (constant polynomial)
- 2x³y² + 5xy - 3: Degree 5 (this is determined by adding the exponents of the highest-degree term, 3 + 2 = 5).
Common Misconceptions about Polynomials
Several misconceptions often arise when identifying polynomials. Let's clarify them:
-
Negative Exponents are Not Allowed: The presence of any negative exponent immediately disqualifies an expression from being a polynomial.
-
Fractional Exponents are Not Allowed: Similar to negative exponents, fractional exponents (like square roots or cube roots) render an expression non-polynomial.
-
Variables in the Exponent are Not Allowed: If the variable appears as an exponent (e.g., 2ˣ), the expression is not a polynomial.
-
Absolute Value Functions are Not Polynomials: The absolute value function introduces non-smoothness, a characteristic not found in polynomials.
Practical Applications of Polynomials
Polynomials are far from mere abstract mathematical concepts. They have wide-ranging applications in various fields:
-
Computer Graphics: Polynomials are used to create curves and surfaces in computer-aided design (CAD) and computer graphics. Bézier curves, for example, are defined using polynomials.
-
Physics and Engineering: Polynomials are frequently used to model physical phenomena, such as the trajectory of a projectile or the motion of a pendulum.
-
Economics and Finance: Polynomial functions can be used to model economic growth, interest calculations, and other financial models.
-
Signal Processing: Polynomials are fundamental in designing digital filters and signal processing algorithms.
-
Numerical Analysis: Polynomials are used in approximation techniques to approximate complex functions, which is incredibly useful in solving equations that cannot be solved analytically.
Advanced Polynomial Concepts (Brief Overview)
Beyond the basics, numerous advanced concepts build upon the foundation of polynomials:
-
Polynomial Division: This involves dividing one polynomial by another, often resulting in a quotient and remainder.
-
Factoring Polynomials: This involves expressing a polynomial as a product of simpler polynomials.
-
Roots of Polynomials: These are the values of the variable that make the polynomial equal to zero. Finding the roots is a crucial aspect of polynomial analysis.
-
Partial Fraction Decomposition: This technique is used to decompose rational functions (fractions of polynomials) into simpler fractions.
-
Taylor and Maclaurin Series: These infinite series use polynomials to approximate functions, providing powerful tools for calculus and analysis.
Conclusion: Mastering Polynomial Identification
Identifying polynomials requires a clear understanding of their defining characteristics: non-negative integer exponents on the variables and coefficients that are constants. By carefully examining the exponents and the overall structure of an algebraic expression, you can confidently distinguish polynomials from other mathematical expressions. This understanding is crucial for further studies in algebra, calculus, and numerous applied fields where polynomials play a vital role. Mastering this fundamental concept opens doors to a deeper comprehension of many advanced mathematical principles and their applications in the real world. Remember to practice identifying polynomials using various examples to solidify your skills. The more you practice, the easier it will become to spot them instantly.
Latest Posts
Latest Posts
-
How Many Feet Is 26 Inches
Apr 05, 2025
-
Actin And Myosin Are What Type Of Biological Molecule
Apr 05, 2025
-
Fluid Part Of Blood After Removal Of Corpuscles Is
Apr 05, 2025
-
Is A Substance In Which Another Substance Is Dissolved
Apr 05, 2025
-
Empirical Formula Calculator For Ionic Compounds
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Which Algebraic Expressions Are Polynomials Check All That Apply . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
