When Multiplying Fractions Do You Cross Multiply
Juapaving
Apr 06, 2025 · 5 min read
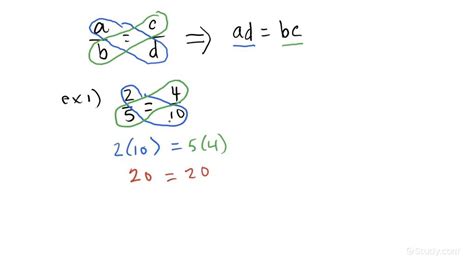
Table of Contents
When Multiplying Fractions, Do You Cross Multiply? A Comprehensive Guide
The question of whether to cross-multiply when multiplying fractions is a common point of confusion for many students. The short answer is: no, you don't cross-multiply when multiplying fractions. Cross-multiplication is a technique used to solve equations with fractions, not to multiply fractions themselves. This article will delve into the correct method of multiplying fractions, explain the purpose of cross-multiplication, and clear up any misconceptions.
Understanding Fraction Multiplication
Multiplying fractions is a fundamental arithmetic operation, and mastering it is crucial for success in higher-level mathematics. The process is straightforward: you multiply the numerators (top numbers) together and then multiply the denominators (bottom numbers) together.
The Formula:
(a/b) * (c/d) = (a * c) / (b * d)
Example:
(1/2) * (3/4) = (1 * 3) / (2 * 4) = 3/8
This simple process is the cornerstone of fraction multiplication. There's no need for any fancy techniques like cross-multiplication. It's all about multiplying the numerators and denominators separately.
The Role of Cross-Multiplication
Cross-multiplication is a method used to solve equations where a fraction is equal to another fraction. It's a shortcut that helps us find the unknown value in such equations.
The Equation:
a/b = c/d
Cross-Multiplication Technique:
To solve for an unknown variable (let's say 'a'), we cross-multiply:
a * d = b * c
Then, we isolate 'a' by dividing both sides by 'd':
a = (b * c) / d
Example:
Solve for 'x':
x/5 = 2/3
Cross-multiply:
3x = 10
Solve for x:
x = 10/3
Cross-multiplication is a valuable tool for solving equations, but it's not applicable to simply multiplying two or more fractions together. Using cross-multiplication when multiplying fractions will yield an incorrect answer.
Common Mistakes and Misconceptions
The confusion between multiplying fractions and cross-multiplication often stems from a misunderstanding of the underlying concepts. Here are some common mistakes:
-
Applying Cross-Multiplication to Fraction Multiplication: This is the most frequent error. Students might mistakenly try to cross-multiply the numerators and denominators, resulting in an incorrect product.
-
Confusing Proportions with Multiplication: While cross-multiplication is relevant when dealing with proportions (equal ratios), it's inappropriate when multiplying fractions independently. The two operations serve different purposes.
-
Ignoring Simplification: After multiplying fractions, it's essential to simplify the result by reducing the fraction to its lowest terms. Failing to simplify leads to an answer that might be correct but not in its simplest form.
Simplifying Fractions Before Multiplication
One strategy to make fraction multiplication easier and more efficient is to simplify before multiplying. This involves canceling out common factors in the numerators and denominators before performing the multiplication.
Example:
(6/10) * (5/12)
Notice that 6 and 12 share a common factor of 6, and 5 and 10 share a common factor of 5. We can simplify:
(6/10) * (5/12) = (3/5) * (1/2) = 3/10
Simplifying beforehand reduces the size of the numbers and makes the calculation less prone to errors. It's a helpful practice to develop.
Multiplying More Than Two Fractions
The process of multiplying fractions remains consistent even when dealing with more than two fractions. You simply multiply all the numerators together and then multiply all the denominators together.
Example:
(1/2) * (3/4) * (2/5) = (1 * 3 * 2) / (2 * 4 * 5) = 6/40
Remember to simplify the result to its lowest terms:
6/40 = 3/20
Multiplying Fractions with Whole Numbers
When multiplying a fraction by a whole number, remember that a whole number can be expressed as a fraction with a denominator of 1.
Example:
3 * (2/5) = (3/1) * (2/5) = 6/5
This allows you to apply the standard fraction multiplication rule.
Multiplying Mixed Numbers
Mixed numbers (a combination of a whole number and a fraction, such as 2 1/2) need to be converted into improper fractions before multiplication.
Example:
2 1/2 * 1 1/3
Convert to improper fractions:
(5/2) * (4/3) = 20/6
Simplify:
20/6 = 10/3
Real-World Applications of Fraction Multiplication
Fraction multiplication isn't just an abstract mathematical concept; it finds numerous applications in real-world scenarios. Here are a few examples:
-
Cooking and Baking: Scaling recipes up or down requires multiplying fractions. For example, if a recipe calls for 1/2 cup of flour and you want to double the recipe, you'd multiply 1/2 by 2.
-
Construction and Engineering: Calculating measurements and material quantities often involves working with fractions.
-
Finance and Budgeting: Determining percentages, calculating discounts, and managing finances frequently require fraction multiplication.
-
Science and Research: Many scientific calculations and experiments utilize fractions and require multiplication.
Beyond the Basics: Advanced Fraction Operations
While this article has focused on the fundamental aspects of multiplying fractions, more advanced concepts build upon this foundation. These include:
-
Multiplying fractions with variables: This extends the concept to algebraic expressions.
-
Multiplying complex fractions: These involve fractions within fractions.
-
Multiplying fractions in various number systems: This includes working with different bases beyond the familiar base-10 system.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is a critical skill that underpins many mathematical operations. While cross-multiplication is a useful technique for solving equations with fractions, it's crucial to remember that it's not used when directly multiplying fractions. By understanding the correct method, simplifying fractions before multiplication, and practicing regularly, you can build a strong foundation in fraction arithmetic. Remember, consistency and practice are key to mastering this important mathematical skill. Always remember to simplify your answers to their lowest terms for the most accurate and efficient solutions. By understanding both the mechanics and the practical applications of fraction multiplication, you can confidently tackle various mathematical challenges and real-world problems that require this essential skill.
Latest Posts
Latest Posts
-
6 Faces 12 Edges And 8 Vertices
Apr 08, 2025
-
What Is The Motor End Plate
Apr 08, 2025
-
How Big Is 18cm In Inches
Apr 08, 2025
-
Two Compounds A And B Have The Formula
Apr 08, 2025
-
Which Cardiac Chamber Has The Thickest Wall
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about When Multiplying Fractions Do You Cross Multiply . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.