When Can You Use Henderson Hasselbalch Equation
Juapaving
Apr 07, 2025 · 6 min read
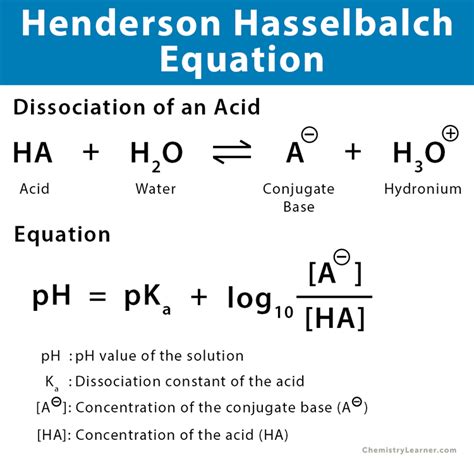
Table of Contents
When Can You Use the Henderson-Hasselbalch Equation? A Comprehensive Guide
The Henderson-Hasselbalch equation is a cornerstone of acid-base chemistry, providing a straightforward way to calculate the pH of a buffer solution. But its application isn't limitless. Understanding when and how to use this equation correctly is crucial for accurate calculations and a deeper understanding of buffer systems. This comprehensive guide will delve into the conditions under which the Henderson-Hasselbalch equation is applicable, its limitations, and alternative approaches when it falls short.
Understanding the Henderson-Hasselbalch Equation
The equation itself is relatively simple:
pH = pKa + log([A⁻]/[HA])
Where:
- pH: The measure of hydrogen ion concentration, indicating the acidity or basicity of the solution.
- pKa: The negative logarithm of the acid dissociation constant (Ka), representing the strength of the acid. A lower pKa indicates a stronger acid.
- [A⁻]: The concentration of the conjugate base.
- [HA]: The concentration of the weak acid.
This equation allows us to predict the pH of a buffer solution, a solution that resists changes in pH upon the addition of small amounts of acid or base. This resistance is crucial in many biological and chemical systems.
Conditions for Using the Henderson-Hasselbalch Equation
The Henderson-Hasselbalch equation isn't a universally applicable formula. Its accuracy relies on several key assumptions:
1. Weak Acid/Weak Base System:
The equation is specifically designed for weak acid-conjugate base or weak base-conjugate acid buffer systems. It does not apply to strong acids or strong bases. Strong acids and bases completely dissociate in solution, making the use of equilibrium constants (and therefore the Henderson-Hasselbalch equation) irrelevant.
2. Negligible Autoprotolysis of Water:
The equation assumes the autoprotolysis of water (the self-ionization of water, 2H₂O ⇌ H₃O⁺ + OH⁻) has a negligible effect on the overall pH. This is generally true for solutions with pH values between 4 and 10. Outside this range, the contribution of water's autoprotolysis becomes significant, and the equation becomes less accurate.
3. Significant Concentrations of Both Acid and Conjugate Base:
The equation works best when the concentrations of both the weak acid (HA) and its conjugate base (A⁻) are relatively high and comparable. Ideally, the ratio [A⁻]/[HA] should be between 0.1 and 10. If the concentration of either the acid or the base is extremely low compared to the other, the equation's accuracy diminishes. This is because the equation relies on the equilibrium between the acid and its conjugate base being established.
4. Ideal Solution Behavior:
The equation assumes ideal solution behavior, meaning that the activity coefficients of the ions are approximately equal to 1. This assumption holds true for dilute solutions but may break down at higher concentrations where intermolecular forces become more significant. In these cases, activity coefficients need to be considered for more accurate calculations.
5. Temperature Considerations:
The pKa value is temperature-dependent. The Henderson-Hasselbalch equation uses a pKa value specific to a given temperature. If the temperature changes significantly, the pKa value must be adjusted accordingly to ensure accuracy. Using a pKa value at a different temperature will lead to an inaccurate pH calculation.
When the Henderson-Hasselbalch Equation is NOT Suitable:
There are several scenarios where the Henderson-Hasselbalch equation should be avoided or used with extreme caution:
1. Strong Acid/Strong Base Solutions:
As mentioned earlier, strong acids and bases completely dissociate. The concept of an equilibrium constant, and thus the pKa value, doesn't apply. The pH of a strong acid or base solution is simply calculated using the concentration of the strong acid or base.
2. Very Dilute Solutions:
In extremely dilute solutions, the autoprotolysis of water can significantly affect the pH, rendering the Henderson-Hasselbalch equation inaccurate. In such cases, a more rigorous approach that considers the water autoprotolysis equilibrium is necessary.
3. Solutions with High Ionic Strength:
In solutions with high ionic strength (high concentration of ions), the activity coefficients of ions deviate significantly from unity. This violates the assumption of ideal solution behavior, making the Henderson-Hasselbalch equation less accurate. In these scenarios, activity coefficients need to be incorporated into the calculations.
4. Polyprotic Acids:
The Henderson-Hasselbalch equation is primarily applicable to monoprotic acids (acids with only one ionizable proton). For polyprotic acids (acids with multiple ionizable protons), multiple equilibrium constants are involved, and a more complex approach is required to calculate the pH. Each ionization step has its own pKa value, and the overall pH depends on the interplay of these multiple equilibria.
5. Non-Aqueous Solutions:
The Henderson-Hasselbalch equation is typically applied to aqueous solutions. In non-aqueous solvents, the equation's applicability depends on the solvent's properties and the behavior of the acid and its conjugate base in that solvent. The pKa value itself might be significantly different in a non-aqueous solvent.
Alternatives to the Henderson-Hasselbalch Equation:
When the Henderson-Hasselbalch equation is not suitable, alternative methods are needed to calculate the pH:
-
Complete equilibrium calculations: For more complex systems, solving the complete equilibrium equations is required. This involves setting up and solving a system of mass balance and charge balance equations along with the relevant equilibrium constant expressions. This approach is more computationally intensive but provides more accurate results, particularly in cases involving multiple equilibria or high ionic strengths.
-
Numerical methods: For complex systems, numerical methods, such as iterative calculations or computer simulations, may be needed to solve the equilibrium equations. Software packages are commonly used for these more complex scenarios.
-
Activity coefficients: In solutions with high ionic strength, activity coefficients must be incorporated into the calculations to account for deviations from ideal solution behavior. Different models, such as the Debye-Hückel equation or its extended versions, are used to estimate activity coefficients.
Practical Applications and Examples
The Henderson-Hasselbalch equation is widely used in various fields:
-
Medicine: Understanding buffer systems is crucial in pharmacology and physiology. The equation helps determine the pH of blood and other bodily fluids and how they respond to changes in acid-base balance.
-
Analytical Chemistry: The equation is essential in titrations and buffer preparation. It helps determine the optimal pH for various chemical reactions.
-
Environmental Science: The equation is used in analyzing the pH of natural water bodies and understanding the effects of pollutants.
-
Chemical Engineering: The equation plays a crucial role in designing and optimizing chemical processes that require specific pH control.
Example: A buffer solution is prepared by mixing 0.1 M acetic acid (pKa = 4.76) and 0.1 M sodium acetate. Using the Henderson-Hasselbalch equation:
pH = pKa + log([A⁻]/[HA]) = 4.76 + log(0.1/0.1) = 4.76
The pH of the buffer is 4.76. This is only accurate if the conditions outlined earlier are met.
Conclusion
The Henderson-Hasselbalch equation is a powerful tool for calculating the pH of buffer solutions, but its applicability is limited by several assumptions. Understanding these limitations is crucial to ensure accurate calculations and avoid misinterpretations. When the assumptions are not met, alternative methods, such as complete equilibrium calculations or numerical methods, must be employed. By understanding both the strengths and limitations of the Henderson-Hasselbalch equation, scientists and engineers can make accurate pH predictions in a wide range of applications. Remember to always carefully consider the conditions of your system before applying this equation.
Latest Posts
Latest Posts
-
How Many Feet Is 22 Inches
Apr 08, 2025
-
Things That Start With A Y
Apr 08, 2025
-
Energy Saved Is Energy Produced Assess The Statement
Apr 08, 2025
-
How Many Acres Is 1 Mile
Apr 08, 2025
-
What Is The Sqaure Root Of 36
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about When Can You Use Henderson Hasselbalch Equation . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.