What's The Square Root Of 29
Juapaving
Mar 26, 2025 · 5 min read
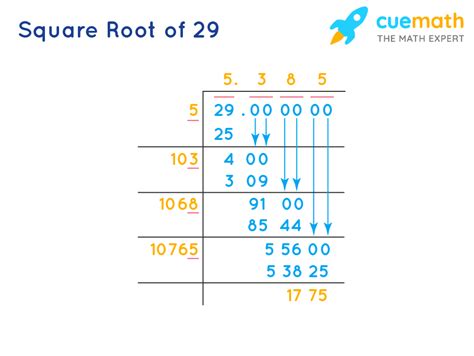
Table of Contents
What's the Square Root of 29? A Deep Dive into Irrational Numbers and Approximation Methods
The seemingly simple question, "What's the square root of 29?", opens a fascinating window into the world of mathematics, specifically the realm of irrational numbers and the various methods used to approximate their values. While a simple calculator will readily provide a decimal approximation, understanding the underlying concepts and techniques offers a richer appreciation for the nature of numbers.
Understanding Square Roots and Irrational Numbers
Before diving into the specifics of √29, let's establish a foundational understanding. The square root of a number, denoted by the symbol √, is a value that, when multiplied by itself, yields the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9.
However, not all square roots result in whole numbers. Numbers like √29 fall into the category of irrational numbers. These are numbers that cannot be expressed as a simple fraction (a ratio of two integers) and their decimal representations are non-repeating and non-terminating. This means the digits after the decimal point go on forever without any pattern.
This inherent characteristic of irrational numbers makes finding their exact value impossible. Instead, we rely on approximation methods to obtain values that are sufficiently accurate for practical purposes.
Methods for Approximating √29
Several methods can approximate the square root of 29. Let's explore some of the most common approaches:
1. Using a Calculator
The simplest and most widely accessible method is using a calculator. A scientific calculator or even a basic calculator will provide a decimal approximation, typically to several decimal places. You'll find that √29 ≈ 5.3851648... This is a convenient method, but it doesn't offer insight into the underlying mathematical principles.
2. The Babylonian Method (or Heron's Method)
This iterative method provides a progressively more accurate approximation with each iteration. It's based on the principle of refining an initial guess through successive calculations.
-
Step 1: Make an initial guess. Since 5² = 25 and 6² = 36, a reasonable initial guess would be 5.
-
Step 2: Improve the guess. The formula for the Babylonian method is: x_(n+1) = 0.5 * (x_n + (29/x_n)), where x_n is the current guess and x_(n+1) is the improved guess.
-
Step 3: Iterate. Repeat Step 2, using the improved guess as the new x_n, until the desired level of accuracy is achieved. Let's perform a few iterations:
- Iteration 1: x_1 = 0.5 * (5 + (29/5)) ≈ 5.4
- Iteration 2: x_2 = 0.5 * (5.4 + (29/5.4)) ≈ 5.385
- Iteration 3: x_3 = 0.5 * (5.385 + (29/5.385)) ≈ 5.38516
As you can see, the approximation converges rapidly towards the actual value of √29.
3. The Newton-Raphson Method
This is another iterative method, similar to the Babylonian method but more generally applicable to finding roots of equations. For finding the square root of a number 'a', the formula becomes: x_(n+1) = 0.5 * (x_n + (a/x_n)). This is essentially the same as the Babylonian method.
4. Linear Interpolation
This method uses the known square roots of numbers close to 29 to estimate the value. Since √25 = 5 and √36 = 6, we can linearly interpolate:
- The difference between 29 and 25 is 4.
- The difference between 36 and 25 is 11.
- The fraction representing the position of 29 between 25 and 36 is 4/11.
- Therefore, an approximate value of √29 is 5 + (4/11) * (6 - 5) ≈ 5.36
This method is less accurate than the iterative methods but provides a quick estimate.
5. Continued Fractions
This elegant method represents irrational numbers as an infinite continued fraction. While the complete representation is infinite, truncating the continued fraction at a certain point provides an approximation. The continued fraction representation of √29 is complex and beyond the scope of this simple explanation, but it offers an alternative approach to approximation.
The Significance of Irrational Numbers
The existence of irrational numbers like √29 has profound implications in mathematics and beyond. They highlight the limitations of representing all numbers using simple fractions and emphasize the richness and complexity of the number system.
Irrational numbers are essential in various fields:
- Geometry: The diagonal of a square with sides of length 1 has a length of √2, an irrational number. Irrational numbers frequently appear in geometric calculations.
- Physics: Many physical phenomena involve irrational numbers in their mathematical descriptions. For example, the ratio of a circle's circumference to its diameter (π) is an irrational number.
- Calculus: Irrational numbers are fundamental in calculus and analysis, where limits and infinite series are often involved.
Practical Applications and Conclusion
While we can't express √29 exactly as a fraction or a terminating decimal, we can approximate it to any desired level of accuracy using methods like the Babylonian or Newton-Raphson methods. These approximations are sufficient for most practical applications in engineering, science, and other fields.
Understanding the concept of irrational numbers and the techniques used to approximate them expands our mathematical knowledge and appreciation of the complexities of numbers. The seemingly simple question of "What's the square root of 29?" reveals a deeper mathematical landscape that is both intriguing and significant. The methods discussed above provide a foundation for tackling more complex mathematical problems involving irrational numbers and demonstrate the power of iterative approaches in finding solutions. Furthermore, the exploration of these approximation techniques enhances problem-solving skills and promotes a deeper understanding of numerical computation. Finally, appreciating the ubiquity of irrational numbers in various fields highlights their importance in our comprehension of the physical world and mathematical constructs.
Latest Posts
Latest Posts
-
Non Perennial Rivers Of India
Mar 29, 2025
-
The Protoplasm And Cytoplasm Of A Plant Are Interchangeable Terms
Mar 29, 2025
-
Convert 1 8 To A Percent
Mar 29, 2025
-
A Weight Is Suspended From A String
Mar 29, 2025
-
Which Is The Correct Formula For The Compound Dinitrogen Monoxide
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 29 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
