Whats The Square Root Of 196
Juapaving
Apr 06, 2025 · 6 min read
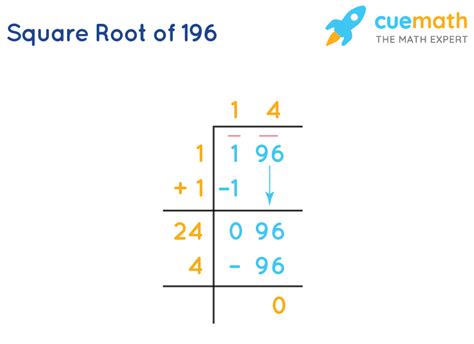
Table of Contents
What's the Square Root of 196? A Deep Dive into Square Roots and Their Applications
The seemingly simple question, "What's the square root of 196?" opens a door to a fascinating world of mathematics, encompassing concepts crucial to various fields, from basic algebra to advanced physics. This article will not only answer that question definitively but will also explore the broader context of square roots, their properties, calculation methods, and their practical applications in diverse real-world scenarios.
Understanding Square Roots: The Basics
Before delving into the square root of 196, let's establish a fundamental understanding of what a square root actually is. The square root of a number is a value that, when multiplied by itself (squared), equals the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. Similarly, the square root of 16 is 4 because 4 x 4 = 16. This is often represented mathematically as √x, where 'x' is the number for which you're finding the square root.
The Square Root of 196: The Answer
Now, to answer the central question: The square root of 196 is 14. This is because 14 multiplied by itself (14 x 14) equals 196.
Methods for Calculating Square Roots
While the square root of 196 is relatively straightforward to determine (especially with readily available calculators), understanding the methods for calculating square roots is crucial for appreciating the underlying mathematical principles. Several methods exist, ranging from simple estimation to complex algorithms.
1. Prime Factorization: This method involves breaking down the number into its prime factors. For 196, the prime factorization is 2² x 7². The square root is then found by taking half of each exponent and multiplying the results: √(2² x 7²) = 2¹ x 7¹ = 14. This method works well for numbers with perfect square factors.
2. Estimation and Trial and Error: This is a practical approach, particularly useful when calculators aren't readily available. You begin by estimating a value (e.g., you might guess 13). Squaring the estimate (13 x 13 = 169) shows it's too low. Adjust your estimate upwards (e.g., to 14). Squaring it (14 x 14 = 196) gives you the correct answer.
3. Babylonian Method (or Heron's Method): This iterative method provides increasingly accurate approximations of square roots. It starts with an initial guess and refines it through successive calculations. The formula is: x_(n+1) = ½ * (x_n + (N/x_n)), where x_n is the current guess, N is the number whose square root is being calculated, and x_(n+1) is the improved guess. This method converges rapidly toward the correct answer.
4. Using a Calculator: Modern calculators readily provide square root calculations. This is the most convenient method for most practical purposes.
The Significance of Square Roots in Mathematics and Beyond
The concept of square roots extends far beyond simple calculations. They form a cornerstone of numerous mathematical concepts and have widespread applications in various fields.
1. Geometry: Square roots are fundamental in geometry, particularly when calculating distances and areas. The Pythagorean theorem, a cornerstone of geometry, relies heavily on square roots: a² + b² = c², where 'c' (the hypotenuse of a right-angled triangle) is calculated using the square root of the sum of the squares of the other two sides ('a' and 'b'). Calculating the diagonal of a square or rectangle directly involves the Pythagorean theorem and hence the use of square roots.
2. Physics: Square roots appear extensively in physics. For instance, in calculating speed, velocity, and acceleration, understanding and applying square roots is crucial. In the field of optics, calculating the refractive index and other optical properties frequently requires square root calculations. Furthermore, the study of motion, especially projectile motion and other vector quantities often utilizes the application of square roots, particularly the Pythagorean theorem in multi-dimensional space.
3. Engineering: Engineers rely heavily on square roots in various calculations. Structural calculations, especially those involving stress, strain, and force analysis, often require the precise calculation of square roots. Similarly, calculations involving electrical circuits frequently include square roots, especially those involving impedance and other alternating current (AC) principles.
4. Finance: Square roots are crucial in finance, especially in portfolio optimization and risk management. Statistical measures like standard deviation, which quantifies the risk associated with investments, use square roots in their calculation.
5. Computer Science: Square roots are essential in computer graphics and image processing, especially for calculating distances between points in 2D and 3D space. Algorithms dealing with matrix transformations and rotations often utilize square root computations. Furthermore, optimization routines and numerical computation algorithms regularly employ methods involving approximations of square roots.
6. Statistics: Calculating standard deviation, a measure of data dispersion, requires taking the square root of the variance. Understanding this allows statisticians to gauge the spread and variability within a dataset.
7. Everyday Applications: While less obvious, square roots are also involved in everyday tasks. For example, calculating the area of a square or the length of the diagonal in a rectangular room utilizes the principles of square roots, even though we may not explicitly perform the calculations manually.
Beyond Perfect Squares: Dealing with Irrational Numbers
It's important to note that not all numbers have perfect square roots – meaning roots that are whole numbers or simple fractions. Many numbers, like 2 or 7, have irrational square roots; meaning their decimal representation goes on infinitely without repeating. These irrational numbers are approximated in calculations, and the level of approximation depends on the context and the required precision of the result.
The square root of 196 is unique in its simplicity because it results in a whole number. Most square roots involve irrational numbers, requiring approximations. Understanding this distinction clarifies the significance of the square root of 196 as a special case.
Conclusion: The Ubiquity and Importance of Square Roots
This deep dive into the square root of 196 has demonstrated that the seemingly simple question opens up a broad spectrum of mathematical concepts and real-world applications. From fundamental geometric principles to complex calculations in physics, engineering, finance, and computer science, the understanding and application of square roots are essential. While readily available calculators simplify the computation, appreciating the methods and significance behind square root calculations provides a more profound understanding of mathematics and its relevance in various aspects of life. The square root of 196, being a perfect square, serves as an accessible entry point to this broader, fascinating world of mathematics. Mastering this fundamental concept unlocks a deeper appreciation of the mathematical underpinnings of numerous fields and enhances problem-solving capabilities across various disciplines.
Latest Posts
Latest Posts
-
What Is The Lcm Of 48 And 32
Apr 07, 2025
-
5 Letter Word With A And S
Apr 07, 2025
-
What Is Dispersion Of Light In Physics
Apr 07, 2025
-
Which Nonmetal Is The Most Reactive
Apr 07, 2025
-
What Distinguishes A Substance From A Mixture
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Whats The Square Root Of 196 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
