What's The Prime Factorization Of 12
Juapaving
Apr 02, 2025 · 5 min read
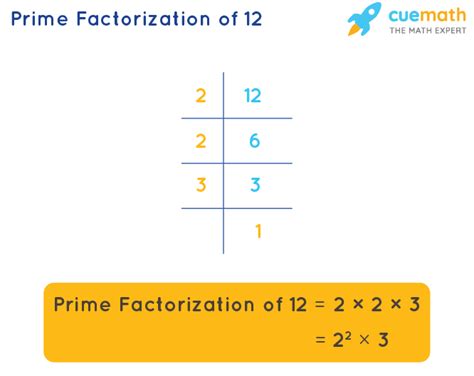
Table of Contents
What's the Prime Factorization of 12? A Deep Dive into Prime Numbers and Factorization
The seemingly simple question, "What's the prime factorization of 12?" opens a door to a fascinating world of number theory, a cornerstone of mathematics. While the answer itself is straightforward, exploring the underlying concepts provides a solid foundation for understanding more complex mathematical ideas. This article will not only answer the question but also delve deep into the meaning of prime numbers, factorization, and the significance of prime factorization in various mathematical applications.
Understanding Prime Numbers
Before tackling the prime factorization of 12, we need to grasp the concept of prime numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This means it's only divisible without a remainder by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered prime because it only has one divisor.
Prime numbers are considered the "building blocks" of all other whole numbers. This fundamental concept is crucial to many areas of mathematics, cryptography, and computer science. The infinitude of prime numbers – the fact that there are infinitely many of them – is a remarkable theorem proven by Euclid centuries ago. This theorem alone underscores the fundamental importance of prime numbers in the fabric of mathematics.
Identifying Prime Numbers
Determining whether a number is prime can be straightforward for smaller numbers, but it becomes increasingly complex as numbers grow larger. The Sieve of Eratosthenes, an ancient algorithm, is a simple and efficient method for finding all prime numbers up to a specified integer. It involves iteratively marking as composite (non-prime) the multiples of each prime, starting with the multiples of 2.
The Importance of Prime Numbers
The importance of prime numbers extends far beyond the realm of pure mathematics. They are fundamental to:
-
Cryptography: Many modern encryption methods, such as RSA, rely heavily on the difficulty of factoring large numbers into their prime components. The security of online transactions and sensitive data hinges on this mathematical principle.
-
Computer Science: Prime numbers play a crucial role in algorithms related to hashing, data structures, and random number generation.
-
Number Theory: Prime numbers form the basis for many advanced theorems and concepts in number theory, a branch of mathematics dedicated to the study of integers and their properties.
-
Coding Theory: Error-correcting codes, essential for reliable data transmission, utilize properties of prime numbers for efficient encoding and decoding.
What is Factorization?
Factorization is the process of breaking down a number into smaller numbers that, when multiplied together, produce the original number. These smaller numbers are called the factors of the original number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Notice that 1 and 12 are factors, as well as 2 and 6, and 3 and 4, illustrating all the possible pairs that multiply to 12.
Different Types of Factorization
There are different types of factorization, depending on the type of numbers involved and the desired outcome. The most common types include:
-
Prime Factorization: Breaking down a number into its prime factors (as explained in the next section).
-
Integer Factorization: Factoring a number into integers.
-
Polynomial Factorization: Factoring a polynomial expression into simpler polynomials.
Prime Factorization of 12: The Solution
Now, let's finally address the initial question: What's the prime factorization of 12?
The prime factorization of 12 is 2 x 2 x 3, or 2² x 3.
This means that 12 can be expressed as the product of its prime factors: 2, 2, and 3. No further factorization into prime numbers is possible. This unique representation is crucial in various mathematical applications.
Methods for Finding Prime Factorization
Several methods can be used to find the prime factorization of a number:
-
Factor Tree: This visual method involves repeatedly dividing a number by its smallest prime factor until only prime numbers remain.
-
Division by Prime Numbers: This method involves systematically dividing the number by the smallest prime numbers (2, 3, 5, 7, etc.) until the result is 1.
-
Using Algorithms: For very large numbers, sophisticated algorithms are used to find their prime factorization. These algorithms are computationally intensive and are the foundation of modern cryptography.
The Uniqueness of Prime Factorization
A fundamental theorem in number theory states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This is known as the Fundamental Theorem of Arithmetic. This uniqueness is essential because it means that any given number has only one prime factorization. This property is instrumental in various mathematical proofs and computations.
Applications of Prime Factorization
Beyond its theoretical significance, prime factorization has practical applications across numerous fields:
-
Simplifying Fractions: Finding the prime factorization of the numerator and denominator of a fraction allows for significant simplification by canceling common factors.
-
Finding the Greatest Common Divisor (GCD): The GCD of two numbers can be efficiently computed using their prime factorizations.
-
Finding the Least Common Multiple (LCM): Similar to finding the GCD, prime factorizations make calculating the LCM of two or more numbers more straightforward.
-
Cryptography (RSA Algorithm): The RSA algorithm, widely used in secure communication, depends on the difficulty of factoring large numbers into their prime components. The security of this algorithm relies on the computational challenge of factoring extremely large numbers, a task that becomes exponentially harder as the numbers increase in size.
Conclusion: More Than Just a Simple Answer
The prime factorization of 12, seemingly a simple calculation, reveals the underlying beauty and power of prime numbers and factorization. This seemingly straightforward question unveils a fundamental concept in mathematics with far-reaching implications across various fields. Understanding prime factorization allows us to grasp a core element of number theory and appreciate its role in shaping our technological world, from secure online transactions to advanced algorithms. The journey from the simple question to the exploration of its underlying principles showcases the depth and elegance of mathematics. Further exploration into prime numbers and their properties is highly encouraged for anyone interested in mathematics, computer science, or cryptography. The world of prime numbers is vast, rich, and continually revealing new wonders.
Latest Posts
Latest Posts
-
A Homogeneous Mixture Is Also Called A
Apr 03, 2025
-
A Substance Formed During A Chemical Reaction
Apr 03, 2025
-
Give The Major Product Of The Following Reaction
Apr 03, 2025
-
An Npn Transistor Is Made Up Of
Apr 03, 2025
-
How Tall Is 48 Inches In Ft
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What's The Prime Factorization Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
