What's The Least Common Multiple Of 6 And 9
Juapaving
May 10, 2025 · 5 min read
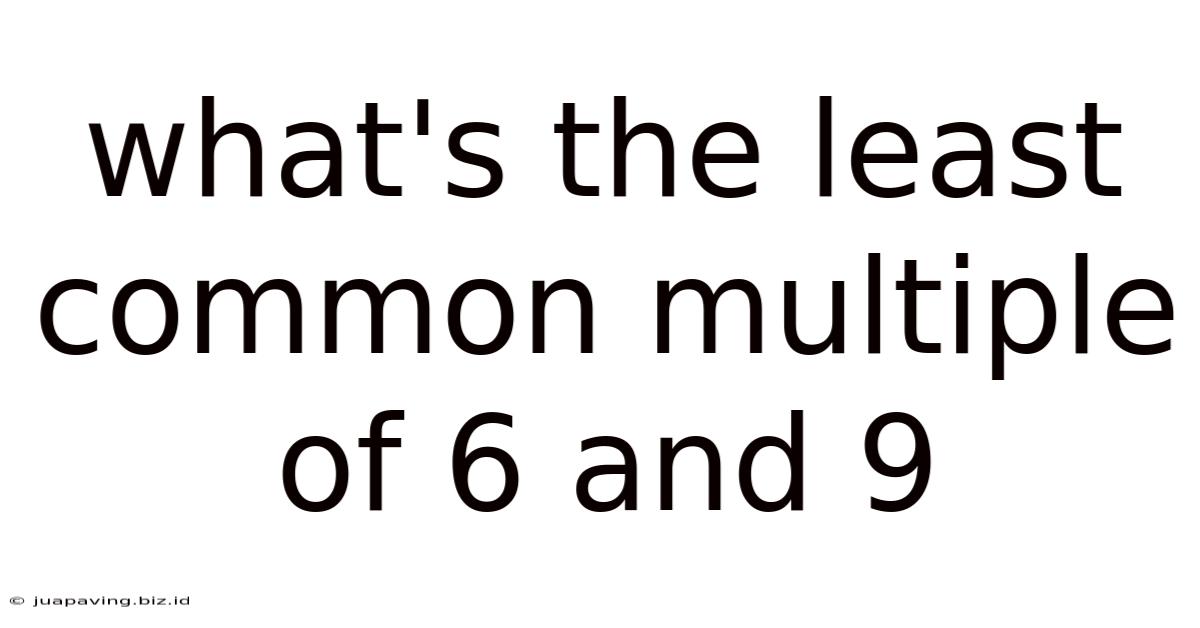
Table of Contents
What's the Least Common Multiple (LCM) of 6 and 9? A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts reveals a fascinating glimpse into number theory and its practical applications. This article will delve into the methods of calculating the LCM of 6 and 9, explore different approaches, and discuss the broader significance of LCMs in various fields.
Understanding Least Common Multiples
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. This concept is fundamental in mathematics and has practical applications across various disciplines.
Methods for Calculating the LCM of 6 and 9
Several methods exist for calculating the LCM, each with its own advantages and insights:
1. Listing Multiples Method
This is the most straightforward approach, especially for smaller numbers like 6 and 9. We simply list the multiples of each number until we find the smallest common multiple.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42...
- Multiples of 9: 9, 18, 27, 36, 45...
By comparing the lists, we can see that the smallest common multiple is 18.
2. Prime Factorization Method
This method is more efficient for larger numbers and offers a deeper understanding of the underlying mathematical structure. It involves breaking down each number into its prime factors.
- Prime factorization of 6: 2 x 3
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2¹
- Highest power of 3: 3²
Therefore, the LCM of 6 and 9 is 2¹ x 3² = 2 x 9 = 18.
3. Greatest Common Divisor (GCD) Method
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both integers without leaving a remainder. The relationship is expressed as:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, let's find the GCD of 6 and 9 using the Euclidean algorithm:
- Divide the larger number (9) by the smaller number (6): 9 ÷ 6 = 1 with a remainder of 3.
- Replace the larger number with the smaller number (6) and the smaller number with the remainder (3): 6 ÷ 3 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 3.
Now, we can calculate the LCM:
LCM(6, 9) = (6 x 9) / 3 = 54 / 3 = 18
This method is particularly useful for larger numbers where prime factorization might be more time-consuming.
Significance of LCM in Real-World Applications
The seemingly simple concept of LCM finds surprising applications in various fields:
1. Scheduling and Time Management
Imagine you have two machines that run on different cycles. One completes a task every 6 hours, and the other every 9 hours. To determine when both machines will complete a task simultaneously, you need to find the LCM of 6 and 9, which is 18. Therefore, both machines will finish together after 18 hours. This concept extends to scheduling meetings, production cycles, and various other time-related scenarios.
2. Fraction Operations
LCM plays a crucial role in adding and subtracting fractions. To add fractions with different denominators, you need to find the LCM of the denominators and convert the fractions to equivalent fractions with the LCM as the common denominator. For example, adding 1/6 and 1/9 requires finding the LCM of 6 and 9 (which is 18), converting the fractions to 3/18 and 2/18, and then adding them to get 5/18.
3. Music Theory
The LCM is used to calculate the least common period of musical rhythms. If one musical phrase has a duration of 6 beats and another has a duration of 9 beats, the LCM (18) represents the shortest time after which both phrases will end simultaneously. This is relevant for composing harmonious musical sequences.
4. Gear Ratios and Mechanical Engineering
In mechanical systems with gears, the LCM helps determine when different gears will align perfectly. This is critical for efficient power transmission and preventing wear and tear.
5. Computer Science and Algorithms
LCM concepts appear in various algorithms, particularly in scheduling tasks in operating systems and optimizing resource allocation.
Expanding the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you simply consider all prime factors from all numbers and take the highest power of each. For the GCD method, you can apply it iteratively, finding the LCM of two numbers first and then finding the LCM of the result with the next number and so on.
For example, let's find the LCM of 6, 9, and 15:
- Prime factorization of 6: 2 x 3
- Prime factorization of 9: 3²
- Prime factorization of 15: 3 x 5
The highest powers are 2¹, 3², and 5¹. Therefore, the LCM(6, 9, 15) = 2 x 9 x 5 = 90.
Conclusion: The Ubiquitous LCM
The least common multiple, while seemingly a simple mathematical concept, reveals itself as a powerful tool with significant applications across various domains. From scheduling tasks to designing mechanical systems and composing music, understanding LCM empowers us to solve practical problems and gain deeper insights into the mathematical structures that govern our world. The simple calculation of the LCM of 6 and 9 serves as a gateway to understanding this broader mathematical concept and its profound implications. Mastering the LCM lays the foundation for tackling more advanced mathematical problems and applying these concepts effectively in diverse real-world situations.
Latest Posts
Latest Posts
-
Volume Of 1 Mole Gas At Stp
May 11, 2025
-
A Car Is Travelling On A Straight Road
May 11, 2025
-
What Is The Fraction Of 40 Percent
May 11, 2025
-
Action Verbs That Begin With E
May 11, 2025
-
Copper Cannot Displace Zinc From Its Salt Solution
May 11, 2025
Related Post
Thank you for visiting our website which covers about What's The Least Common Multiple Of 6 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.