What's The Lcm Of 18 And 24
Juapaving
May 13, 2025 · 5 min read
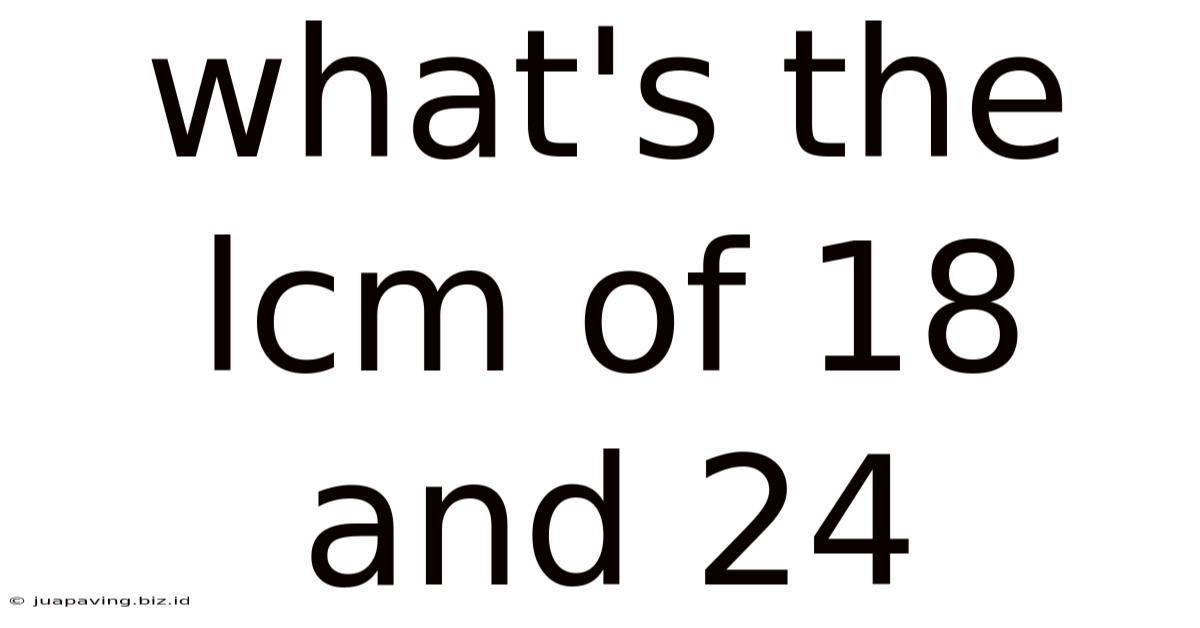
Table of Contents
What's the LCM of 18 and 24? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) might seem like a simple arithmetic problem, but understanding the concept and its various applications extends far beyond basic calculations. This article delves deep into determining the LCM of 18 and 24, exploring multiple methods, and showcasing the practical significance of LCM in various fields. We'll also touch upon related concepts like greatest common divisor (GCD) and their interconnectedness.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
This concept is crucial in numerous applications, from scheduling problems to simplifying fractions and solving equations. It's a fundamental building block in number theory and algebra.
Methods for Finding the LCM of 18 and 24
Several methods can be employed to calculate the LCM of 18 and 24. Let's explore the most common approaches:
1. Listing Multiples Method
This is the most straightforward method, especially for smaller numbers. We list the multiples of both 18 and 24 until we find the smallest multiple common to both lists:
- Multiples of 18: 18, 36, 54, 72, 90, 108, 126, 144, 162, 180...
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, 240...
By comparing the lists, we see that the smallest common multiple is 72. Therefore, the LCM(18, 24) = 72.
This method is effective for smaller numbers but becomes cumbersome and inefficient for larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present in either factorization.
- Prime factorization of 18: 2 x 3²
- Prime factorization of 24: 2³ x 3
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3² = 9
Multiplying these highest powers together: 8 x 9 = 72. Therefore, LCM(18, 24) = 72.
This method is generally preferred for its efficiency and systematic approach, especially when dealing with larger numbers.
3. Using the GCD (Greatest Common Divisor)
The LCM and GCD are closely related. We can use the GCD to find the LCM using the following formula:
LCM(a, b) = (a x b) / GCD(a, b)
First, let's find the GCD of 18 and 24 using the Euclidean algorithm:
- Divide 24 by 18: 24 = 18 x 1 + 6
- Divide 18 by the remainder 6: 18 = 6 x 3 + 0
The last non-zero remainder is the GCD, which is 6.
Now, using the formula:
LCM(18, 24) = (18 x 24) / 6 = 432 / 6 = 72
This method provides a concise and elegant way to calculate the LCM, especially when the GCD is readily available or easily calculated.
Applications of LCM
The concept of LCM extends far beyond simple mathematical exercises. It has practical applications in various fields:
1. Scheduling Problems
Imagine you have two events that repeat at different intervals. LCM helps determine when these events will coincide. For instance, if event A occurs every 18 days and event B every 24 days, they will coincide every 72 days (LCM(18, 24)).
2. Fraction Addition and Subtraction
Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators. This ensures that the fractions are expressed in terms of equivalent fractions with the same denominator, simplifying the addition or subtraction process.
3. Gear Ratios and Mechanical Systems
In mechanical engineering, LCM is used in determining gear ratios and synchronizing rotating components in machinery. The LCM ensures smooth operation by determining the least common multiple of rotational speeds.
4. Music Theory
LCM is used in music theory to determine the least common multiple of rhythmic patterns, which is useful in understanding and composing complex rhythmic structures.
5. Computer Science
LCM finds applications in algorithms and data structures. For example, it plays a role in solving synchronization problems in concurrent programming and scheduling tasks in operating systems.
6. Chemistry
In stoichiometry, the LCM can be helpful in balancing chemical equations, where the coefficients represent the relative amounts of reactants and products. Ensuring that the number of atoms of each element is the same on both sides requires finding the LCM of various ratios.
Conclusion: The Significance of LCM
The seemingly simple calculation of the LCM of 18 and 24, which we found to be 72, unveils a fundamental concept with far-reaching applications. From everyday scheduling to complex engineering problems, understanding and applying the LCM is crucial in various fields. Mastering this concept enhances problem-solving skills and provides a deeper appreciation for the interconnectedness of mathematical principles. The different methods highlighted – listing multiples, prime factorization, and using the GCD – offer diverse approaches, enabling you to choose the most suitable method based on the numbers involved and your preferred approach. The power of LCM lies not just in its calculation but in its practical implications across diverse domains, solidifying its importance in mathematics and beyond. Remember that this is just a glimpse into the world of LCM; further exploration will reveal its profound impact across numerous mathematical and real-world scenarios.
Latest Posts
Latest Posts
-
How Do You Calculate Thermal Energy
May 13, 2025
-
Which Of The Following Statements About Hard Water Is True
May 13, 2025
-
Proximal Convoluted Tubule Vs Distal Convoluted Tubule
May 13, 2025
-
Contraction Of The Cremaster And Dartos Muscles
May 13, 2025
-
What Type Of Cells Have The Most Mitochondria
May 13, 2025
Related Post
Thank you for visiting our website which covers about What's The Lcm Of 18 And 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.