What Percentage Is 1/3 Of 100
Juapaving
May 09, 2025 · 5 min read
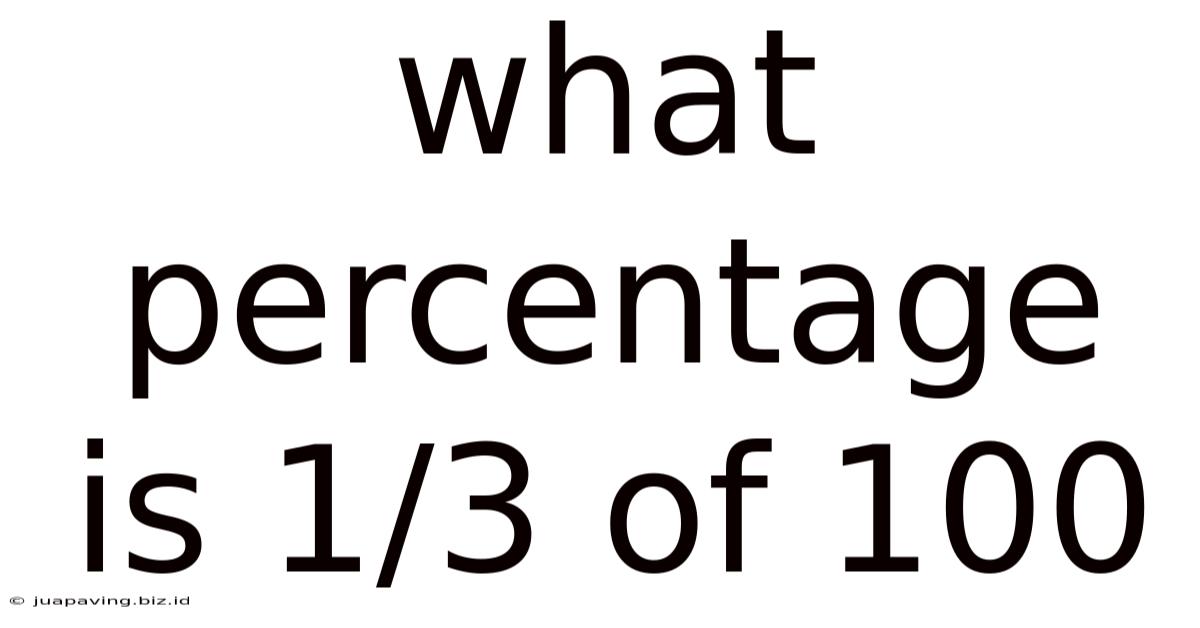
Table of Contents
What Percentage is 1/3 of 100? A Deep Dive into Fractions, Percentages, and Practical Applications
Many of us encounter percentage calculations in our daily lives, from calculating sales tax and discounts to understanding financial reports and statistical data. One common question that often arises involves converting fractions into percentages. This article delves into the specifics of determining what percentage 1/3 represents of 100, exploring the underlying mathematical concepts, practical applications, and offering helpful tips for tackling similar percentage problems.
Understanding Fractions and Percentages
Before diving into the calculation, let's clarify the fundamental concepts of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts you have, and the denominator indicates the total number of parts that make up the whole. For example, in the fraction 1/3, 1 is the numerator and 3 is the denominator. This means we have one part out of a total of three equal parts.
Percentages: A percentage is a way of expressing a fraction or decimal as a portion of 100. The percentage symbol (%) signifies "out of 100" or "per hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Calculating the Percentage: 1/3 of 100
To determine what percentage 1/3 represents of 100, we need to convert the fraction 1/3 into a percentage. This involves two primary methods:
Method 1: Using the Proportion Method
This method utilizes the concept of proportions. We can set up a proportion to solve for the unknown percentage (x):
1/3 = x/100
To solve for x, we cross-multiply:
1 * 100 = 3 * x
100 = 3x
Now, divide both sides by 3:
x = 100/3
x ≈ 33.333...
Therefore, 1/3 of 100 is approximately 33.33%. The three repeating decimal indicates that this is a recurring decimal, meaning the '3' after the decimal point continues infinitely.
Method 2: Converting the Fraction to a Decimal and then to a Percentage
This method involves two steps:
-
Convert the fraction to a decimal: Divide the numerator (1) by the denominator (3):
1 ÷ 3 ≈ 0.333...
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%):
0.333... * 100 ≈ 33.33%
Again, we arrive at the approximate value of 33.33%.
Rounding and Precision
It's important to note that the result, 33.33%, is an approximation. The exact value of 1/3 as a decimal is a non-terminating, repeating decimal (0.333...). When dealing with percentages in practical applications, you'll often need to round the result to a specific number of decimal places based on the required level of precision. For most purposes, rounding to two decimal places (33.33%) is sufficient. However, in situations demanding higher accuracy, you might use more decimal places or express the answer as a fraction (33 1/3%).
Practical Applications of Percentage Calculations
Understanding percentage calculations, particularly converting fractions to percentages, is crucial in various real-world scenarios:
-
Retail and Sales: Calculating discounts, sales tax, profit margins, and markups all involve percentage calculations. For example, a store offering a 1/3 discount on an item would reduce the price by approximately 33.33%.
-
Finance: Analyzing financial statements, calculating interest rates, understanding loan repayments, and tracking investment returns require a strong grasp of percentages. Understanding how much of your investment portfolio is in different asset classes is vital and often represented as percentages.
-
Data Analysis and Statistics: Percentages are frequently used to represent data proportions in charts, graphs, and reports. For example, survey results often present data in percentage form to show the proportion of respondents who chose each option.
-
Science and Engineering: Percentage calculations are used in various scientific and engineering fields. For example, expressing the concentration of a solution or the efficiency of a machine often uses percentages.
-
Everyday Life: Many everyday tasks involve calculating percentages. For example, tipping in a restaurant, determining the percentage of a task completed, or calculating the percentage of calories consumed from different food groups.
Expanding on Fraction to Percentage Conversions
While we focused on 1/3 of 100, the process for converting any fraction to a percentage remains consistent:
- Divide the numerator by the denominator to obtain the decimal equivalent.
- Multiply the decimal by 100 and add the percentage symbol (%) to obtain the percentage equivalent.
For example:
- 2/5: 2 ÷ 5 = 0.4; 0.4 * 100 = 40%
- 3/4: 3 ÷ 4 = 0.75; 0.75 * 100 = 75%
- 5/8: 5 ÷ 8 = 0.625; 0.625 * 100 = 62.5%
Tips for Mastering Percentage Calculations
-
Practice regularly: The more you practice, the more comfortable you'll become with percentage calculations. Try solving various percentage problems to build your skills.
-
Use calculators efficiently: Calculators can be helpful, especially when dealing with complex fractions or decimals. Familiarize yourself with your calculator's functions for percentage calculations.
-
Understand the underlying concepts: Ensure you have a clear understanding of fractions, decimals, and the relationship between them and percentages. This foundational knowledge will make solving problems much easier.
-
Break down complex problems: If you encounter a complex problem, break it down into smaller, more manageable steps. This approach can help you avoid errors and improve your understanding.
-
Check your answers: Always check your answers to ensure accuracy. Use estimation techniques to verify if your answer is reasonable.
Conclusion: The Significance of 33.33%
In conclusion, 1/3 of 100 is approximately 33.33%. Understanding this conversion, and the underlying principles of fractions and percentages, is crucial for navigating numerous real-world situations. Mastering these calculations empowers you to confidently tackle challenges in various fields, from finance and retail to data analysis and everyday life. Remember that practice and a strong understanding of the fundamentals are key to mastering percentage calculations. By consistently applying these techniques and tips, you can improve your numerical skills and enhance your ability to interpret and utilize percentage data effectively.
Latest Posts
Latest Posts
-
Having Two Different Alleles For A Gene
May 10, 2025
-
Tiny Holes On Leaves Are Called
May 10, 2025
-
What Is The Lcm Of 30 And 18
May 10, 2025
-
What Is The Value Of K In Coulombs Law
May 10, 2025
-
How Many 1 In A Gram
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 1/3 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.