What Percent Of 250 Is 70
Juapaving
May 13, 2025 · 4 min read
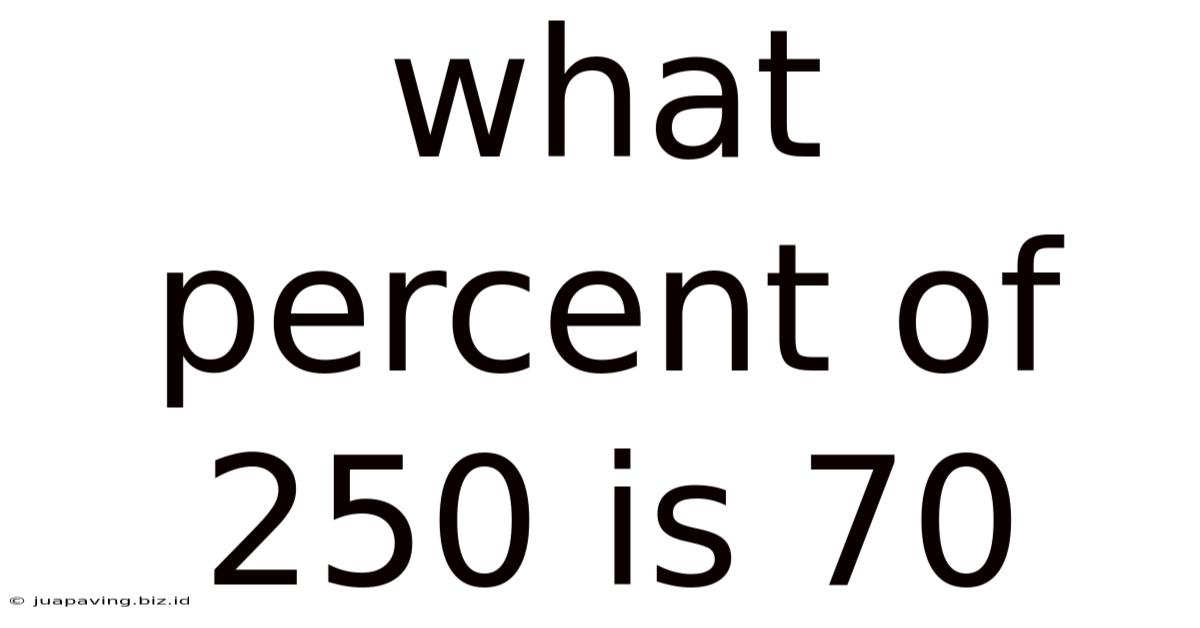
Table of Contents
What Percent of 250 is 70? A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill with wide-ranging applications in various aspects of life, from calculating discounts and tax rates to analyzing data and understanding financial reports. This article will not only answer the question "What percent of 250 is 70?" but will also provide a comprehensive guide to percentage calculations, equipping you with the tools to solve similar problems independently.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to 50/100 or 1/2.
Calculating Percentages: The Formula
The core formula for calculating percentages is:
(Part / Whole) x 100 = Percentage
Where:
- Part: This is the value you want to express as a percentage of the whole.
- Whole: This is the total value.
- Percentage: This is the result, expressed as a percentage.
Solving "What Percent of 250 is 70?"
Let's apply the formula to answer our main question:
Part = 70 Whole = 250
Using the formula:
(70 / 250) x 100 = Percentage
-
Divide the part by the whole: 70 / 250 = 0.28
-
Multiply the result by 100: 0.28 x 100 = 28
Therefore, 70 is 28% of 250.
Alternative Methods for Percentage Calculation
While the primary formula is straightforward, several alternative methods can simplify percentage calculations, especially in different contexts.
Method 1: Using Proportions
Proportions provide a visual and intuitive approach to solving percentage problems. We can set up a proportion:
70/250 = x/100
Cross-multiplying:
250x = 7000
Solving for x:
x = 7000 / 250 = 28
Therefore, x = 28%, confirming our previous result.
Method 2: Using Decimal Equivalents
Percentages can be easily converted to decimals by dividing by 100. Conversely, decimals can be converted to percentages by multiplying by 100. This method is particularly helpful when using calculators or spreadsheets.
To find what percent 70 is of 250:
-
Divide 70 by 250: 70 / 250 = 0.28
-
Multiply the decimal by 100: 0.28 x 100 = 28%
Method 3: Using a Calculator
Most calculators have a percentage function (%) that simplifies the process significantly. Simply enter "70 ÷ 250 =" and then press the "%" button. The result should be 28.
Practical Applications of Percentage Calculations
Understanding percentage calculations has numerous practical applications in various fields:
1. Finance and Budgeting:
- Interest rates: Calculating simple and compound interest.
- Discounts and sales tax: Determining the final price after discounts or adding sales tax.
- Investment returns: Analyzing investment performance.
- Budget allocation: Distributing funds across different budget categories.
2. Data Analysis and Statistics:
- Data representation: Visualizing data using percentage charts and graphs (pie charts, bar graphs).
- Statistical analysis: Calculating percentages to interpret and analyze data sets.
- Probability and risk assessment: Expressing probabilities and risks as percentages.
3. Everyday Life:
- Tip calculations: Determining the appropriate tip amount in restaurants.
- Grocery shopping: Comparing prices and discounts on products.
- Cooking and baking: Adjusting recipe quantities based on percentages.
Advanced Percentage Problems and Solutions
Let's explore some more complex percentage problems and how to solve them:
Problem 1: Finding the Whole when given the Percentage and Part
- Example: 30% of a number is 60. What is the number?
We can set up the equation:
0.30 * x = 60
Solving for x:
x = 60 / 0.30 = 200
Therefore, the number is 200.
Problem 2: Finding the Percentage Increase or Decrease
- Example: A product's price increased from $50 to $65. What is the percentage increase?
-
Find the difference: $65 - $50 = $15
-
Divide the difference by the original price: $15 / $50 = 0.30
-
Multiply by 100 to express as a percentage: 0.30 x 100 = 30%
Therefore, the price increased by 30%.
Problem 3: Calculating Percentage Change with Negative Values
- Example: A stock price dropped from $100 to $80. What is the percentage decrease?
-
Find the difference: $100 - $80 = $20
-
Divide the difference by the original price: $20 / $100 = 0.20
-
Multiply by 100: 0.20 x 100 = 20%
The stock price decreased by 20%.
Conclusion
Mastering percentage calculations is crucial for success in various aspects of life. From simple calculations like finding what percent of 250 is 70 to more complex problems involving percentage increases, decreases, and finding the whole, the techniques outlined in this article provide a solid foundation. Remember to practice regularly and apply these methods to real-world scenarios to reinforce your understanding and build confidence in your ability to tackle any percentage-related problem you may encounter. By understanding the underlying principles and utilizing the different calculation methods, you'll be well-equipped to navigate the world of percentages with ease and accuracy.
Latest Posts
Latest Posts
-
Money Needed To Start A Business Is Called
May 13, 2025
-
What Are The End Products Of Starch Digestion
May 13, 2025
-
What Are Polymers Of Amino Acids
May 13, 2025
-
The Largest Of The Tarsal Bones Is The
May 13, 2025
-
What Is Anything That Takes Up Space And Has Mass
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 250 Is 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.