What Percent Of 200 Is 75
Juapaving
May 10, 2025 · 4 min read
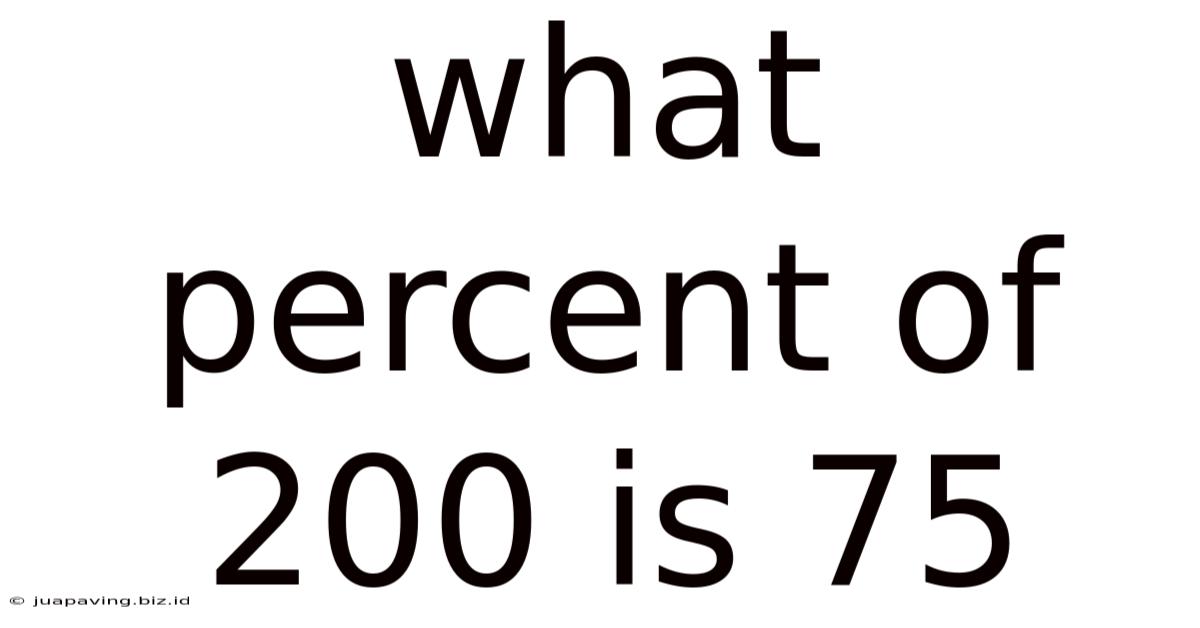
Table of Contents
What Percent of 200 is 75? A Comprehensive Guide to Percentage Calculations
Finding what percentage one number represents of another is a fundamental skill in mathematics with widespread applications in various fields, from finance and budgeting to statistics and data analysis. This comprehensive guide will delve into how to calculate what percent of 200 is 75, explaining the process step-by-step and providing valuable insights into the underlying concepts of percentages. We'll also explore various methods for solving percentage problems and highlight the importance of understanding percentages in everyday life.
Understanding Percentages
Before we dive into the specific problem, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Method 1: Using the Proportion Method
This is a classic and intuitive method for solving percentage problems. We set up a proportion, equating two ratios:
- Ratio 1: The part to the whole (75 to 200)
- Ratio 2: The percentage to 100 (x% to 100)
Our proportion looks like this:
75/200 = x/100
To solve for 'x', we cross-multiply:
75 * 100 = 200 * x
7500 = 200x
Now, divide both sides by 200 to isolate 'x':
x = 7500 / 200
x = 37.5
Therefore, 75 is 37.5% of 200.
Method 2: Using the Decimal Method
This method involves converting the percentage to a decimal and then performing a simple multiplication.
First, we need to express the ratio of the part to the whole as a decimal:
75 / 200 = 0.375
Next, we convert this decimal to a percentage by multiplying by 100:
0.375 * 100 = 37.5%
Thus, we arrive at the same answer: 75 is 37.5% of 200.
Method 3: Using the Formula Method
A more direct approach uses the percentage formula:
Percentage = (Part / Whole) * 100
In our case:
Part = 75 Whole = 200
Plugging the values into the formula:
Percentage = (75 / 200) * 100
Percentage = 0.375 * 100
Percentage = 37.5%
Again, the result confirms that 75 is 37.5% of 200.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous everyday situations:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, determining the discount on a sale item, understanding loan interest, or calculating the tip at a restaurant involve percentage computations.
-
Statistics and Data Analysis: Percentages are essential for interpreting data and presenting findings. They allow us to express proportions, trends, and relationships in a clear and concise way. For instance, analyzing survey results, understanding market shares, or interpreting economic indicators often involves working with percentages.
-
Science: Percentage calculations are frequently used in scientific experiments to express concentrations, yields, and error rates. For instance, measuring the purity of a chemical compound, determining the efficiency of a process, or analyzing the results of clinical trials often rely on percentage calculations.
-
Everyday Life: From calculating sales tax to figuring out the percentage of a task completed, percentages play a vital role in our daily routines. Understanding them enables us to make informed decisions, manage our finances, and solve everyday problems effectively.
Common Percentage Calculation Mistakes to Avoid
While percentage calculations might seem straightforward, several common mistakes can lead to inaccurate results:
-
Incorrect Order of Operations: Remember to follow the order of operations (PEMDAS/BODMAS) when solving complex problems involving percentages. This ensures you perform the calculations in the correct sequence, preventing errors.
-
Confusing Part and Whole: Clearly identify the "part" and the "whole" in the problem. Mixing them up will lead to an incorrect answer.
-
Improper Decimal Conversion: Carefully convert decimals to percentages and vice-versa. Incorrect conversions can drastically affect the final result.
Advanced Percentage Problems and Solutions
Let's explore some more complex scenarios involving percentages:
Example 1: Finding the Whole when the Part and Percentage are Known
-
Problem: 25% of a number is 50. What is the number?
-
Solution: We can set up a proportion: 25/100 = 50/x. Solving for x, we get x = 200.
Example 2: Finding the Percentage Increase or Decrease
-
Problem: A product's price increased from $100 to $125. What is the percentage increase?
-
Solution: The increase is $25. The percentage increase is (25/100) * 100 = 25%.
Example 3: Calculating Compound Interest
Compound interest involves earning interest on both the principal amount and the accumulated interest. Calculating compound interest requires understanding exponential growth and involves more complex formulas.
Mastering Percentage Calculations for Success
Proficiency in percentage calculations is a valuable skill applicable across various domains. By understanding the fundamental concepts and employing the different methods discussed, you can confidently tackle percentage problems and make informed decisions in both academic and real-world settings. Practice regularly, focus on avoiding common errors, and explore more complex problems to enhance your skillset and unlock the full potential of percentage calculations. Remember that consistent practice is key to mastering any mathematical concept. The more you practice, the more comfortable and proficient you will become with solving percentage problems of varying complexity. This mastery will equip you with a valuable tool applicable in numerous facets of life, from personal finance to professional success.
Latest Posts
Latest Posts
-
Why Are Vitamins And Minerals Referred To As Micronutrients
May 10, 2025
-
How Many Centimeters In 20 Meters
May 10, 2025
-
The Only Metal That Is Liquid At Room Temperature
May 10, 2025
-
The Element That Has The Atomic Number 17 Is
May 10, 2025
-
When Both Demand And Supply Change Simultaneously
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 200 Is 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.