What Percent Of 120 Is 90
Juapaving
May 12, 2025 · 4 min read
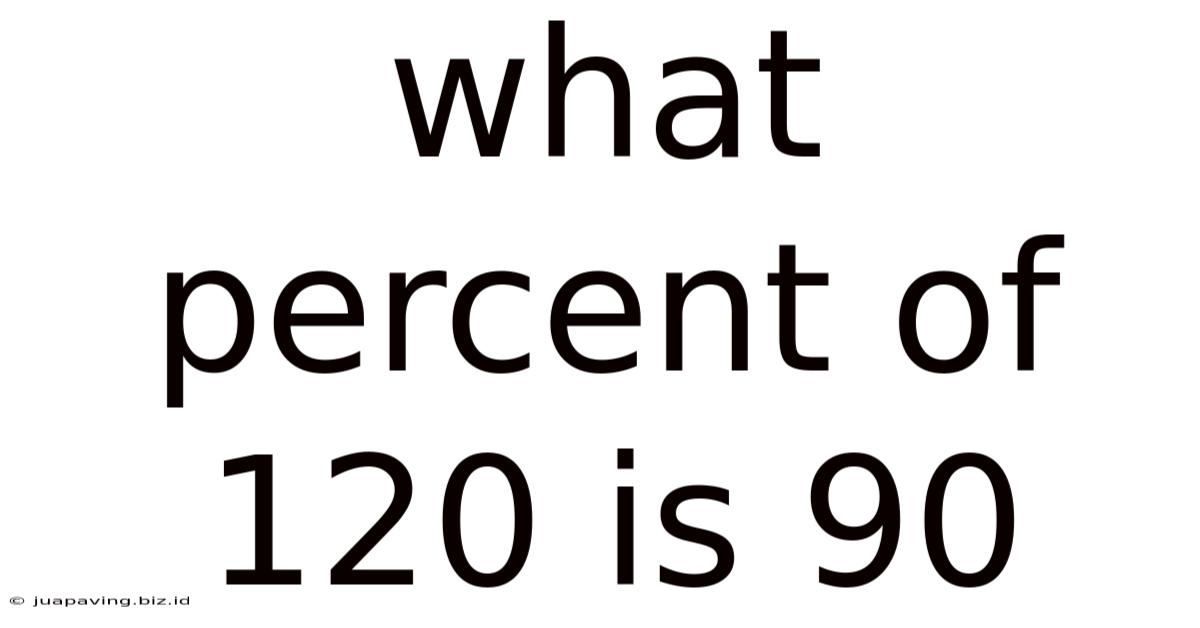
Table of Contents
What Percent of 120 is 90? A Comprehensive Guide to Percentage Calculations
This article delves into the question: "What percent of 120 is 90?" We'll not only solve this specific problem but also explore the broader concept of percentages, providing you with the tools and understanding to tackle similar calculations with ease. We'll cover various methods, including the formula method, the proportion method, and even a quick shortcut for simple calculations. Furthermore, we’ll touch upon the practical applications of percentage calculations in everyday life.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent" or "per hundred." Percentages are used extensively in various fields, including finance, statistics, science, and everyday life, to express proportions, rates, or changes. For instance, understanding percentages is crucial for calculating discounts, taxes, interest rates, and more.
Method 1: The Formula Method
The most straightforward approach to determining what percent of 120 is 90 involves using a fundamental percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 90 (the value we're considering as a part of the whole)
- Whole: 120 (the total value)
Let's plug these values into the formula:
(90 / 120) * 100% = 75%
Therefore, 90 is 75% of 120.
Method 2: The Proportion Method
The proportion method offers an alternative way to solve the problem. This method sets up a proportion using two equivalent ratios:
x / 100 = 90 / 120
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
120x = 90 * 100
120x = 9000
x = 9000 / 120
x = 75
Therefore, again, we find that 90 is 75% of 120.
Method 3: Simplifying Fractions (Shortcut)
For simpler calculations, you can simplify the fraction before multiplying by 100%. This method is particularly useful when dealing with numbers that share common factors.
Let's simplify the fraction 90/120:
90/120 can be simplified by dividing both numerator and denominator by their greatest common divisor, which is 30. This results in:
90 ÷ 30 = 3
120 ÷ 30 = 4
The simplified fraction is 3/4. Now, we convert this fraction to a percentage:
(3/4) * 100% = 75%
Practical Applications of Percentage Calculations
Understanding percentage calculations is a vital life skill. Here are some everyday examples where this knowledge proves invaluable:
1. Calculating Discounts:
Imagine a shirt priced at $120 is on sale with a 25% discount. To calculate the discount amount, we perform the following calculation:
$120 * 0.25 = $30
The discount is $30, making the sale price $90.
2. Determining Tax Amounts:
If you purchase an item for $90 and the sales tax is 6%, the tax amount is:
$90 * 0.06 = $5.40
The total cost including tax is $90 + $5.40 = $95.40.
3. Calculating Interest Earned or Paid:
Suppose you deposit $120 into a savings account that earns 5% annual interest. After one year, the interest earned would be:
$120 * 0.05 = $6
Your total balance would be $126.
4. Understanding Grade Percentages:
In education, your grade is often expressed as a percentage. For example, if you answered 90 questions correctly out of 120, your score is 75%, as demonstrated in our original problem.
5. Analyzing Statistical Data:
Percentages play a critical role in interpreting statistical data. They enable the representation of proportions and trends in a clear and concise manner. For example, understanding that 75% of survey respondents preferred a certain product can significantly influence business decisions.
Advanced Percentage Calculations: Finding the Whole
While the focus has been on finding the percentage, the reverse problem is equally important. Let's say you know that 75% of a certain number is 90. How do you find the original number (the whole)? We can use the following formula:
Whole = Part / (Percentage / 100%)
Plugging in our values:
Whole = 90 / (75% / 100%) = 90 / 0.75 = 120
Conclusion
Calculating percentages is a fundamental skill with numerous applications in daily life and various professional settings. The methods discussed—the formula method, the proportion method, and the simplification technique—offer various approaches to solve percentage problems effectively. Mastering these techniques empowers you to confidently tackle percentage calculations, improving your analytical skills and decision-making abilities in diverse contexts. Remember to practice these techniques regularly to build your proficiency and become more comfortable with these essential mathematical operations. By understanding the core principles behind percentages, you'll not only be able to answer questions like "What percent of 120 is 90?" but also tackle many more complex percentage-related challenges with ease and confidence.
Latest Posts
Latest Posts
-
Number In Words From 1 To 100
May 14, 2025
-
What Is 96 Inches In Feet
May 14, 2025
-
What Percentage Is 35 Out Of 40
May 14, 2025
-
Electricity Is Measured In What Unit
May 14, 2025
-
Is A Pencil A Conductor Or Insulator
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 120 Is 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.