What Percent Of 10 Is 8
Juapaving
Apr 16, 2025 · 4 min read
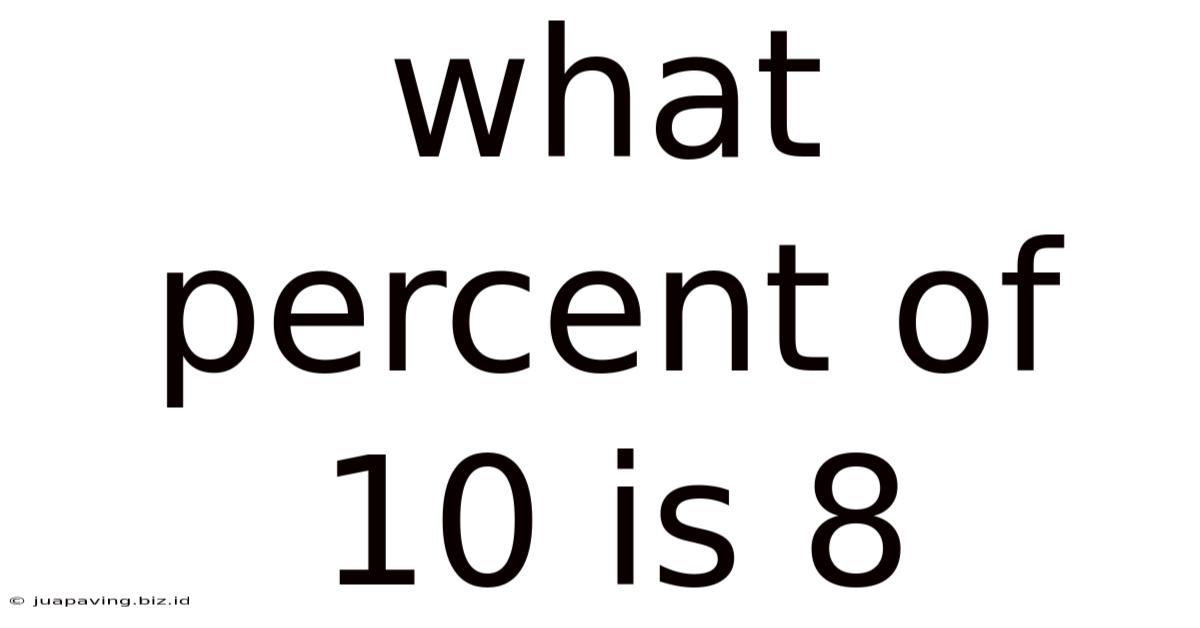
Table of Contents
What Percent of 10 is 8? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percent of 10 is 8?", opens the door to a fascinating exploration of percentage calculations, their applications in everyday life, and how to approach similar problems with confidence. While the answer might seem immediately obvious to some, understanding the underlying principles is crucial for tackling more complex percentage problems. This article will not only provide the solution but also delve into the methods, variations, and real-world applications of percentage calculations.
Understanding Percentages: The Basics
Before diving into the specific problem, let's establish a firm understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100". For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Percentages are used extensively in various fields, including:
- Finance: Interest rates, discounts, tax calculations, profit margins.
- Science: Data analysis, statistical representation, experimental results.
- Everyday Life: Sales, tips, recipe adjustments, survey results.
Mastering percentage calculations is an invaluable skill applicable across numerous contexts.
Calculating "What Percent of 10 is 8?"
Now, let's tackle the core question: What percent of 10 is 8? There are several ways to approach this problem:
Method 1: The Proportion Method
This method uses the concept of proportions to solve the problem. We can set up a proportion where x represents the unknown percentage:
x/100 = 8/10
To solve for x, we cross-multiply:
10x = 800
Then, divide both sides by 10:
x = 80
Therefore, 8 is 80% of 10.
Method 2: The Decimal Method
This method involves converting the fraction 8/10 into a decimal and then multiplying by 100 to express it as a percentage.
First, we express 8 as a fraction of 10: 8/10
Next, we convert this fraction to a decimal by dividing 8 by 10: 8 ÷ 10 = 0.8
Finally, we multiply the decimal by 100 to express it as a percentage: 0.8 x 100 = 80%
Thus, we again arrive at the conclusion that 8 is 80% of 10.
Method 3: Using a Formula
A more general formula for percentage calculations is:
Percentage = (Part / Whole) x 100
In this case:
Part = 8 Whole = 10
Percentage = (8 / 10) x 100 = 80%
Real-World Applications and Variations
The ability to calculate percentages is essential in many real-world scenarios. Let's explore some examples and variations:
Example 1: Sales Discounts
A store offers a 20% discount on an item originally priced at $50. How much is the discount?
We can use the formula:
Discount = (Percentage / 100) x Original Price
Discount = (20 / 100) x $50 = $10
The discount is $10.
Example 2: Calculating Tax
A 6% sales tax is added to a $100 purchase. How much is the tax?
Tax = (Percentage / 100) x Purchase Price
Tax = (6 / 100) x $100 = $6
The sales tax is $6.
Example 3: Finding the Whole When a Percentage is Known
If 25% of a number is 5, what is the number?
Let's use the formula, rearranging it to solve for the "Whole":
Whole = (Part / Percentage) x 100
Whole = (5 / 25) x 100 = 20
The number is 20.
Example 4: Percentage Increase or Decrease
Calculating percentage change involves finding the difference between two values and expressing it as a percentage of the original value.
For example, if a stock price increases from $10 to $12, the percentage increase is:
Percentage Increase = [(New Value - Original Value) / Original Value] x 100
Percentage Increase = [(12 - 10) / 10] x 100 = 20%
Similarly, if the price decreases from $12 to $10, the percentage decrease would be:
Percentage Decrease = [(Original Value - New Value) / Original Value] x 100
Percentage Decrease = [(12 - 10) / 12] x 100 ≈ 16.67%
Tips for Mastering Percentage Calculations
- Practice Regularly: The more you practice, the more comfortable you'll become with percentage calculations.
- Understand the Concepts: Focus on understanding the underlying principles rather than simply memorizing formulas.
- Use Different Methods: Try solving problems using multiple methods to reinforce your understanding.
- Check Your Work: Always verify your answers to ensure accuracy.
- Utilize Online Resources: Many online resources, including calculators and tutorials, can assist you in learning and practicing percentage calculations.
Conclusion
Determining "what percent of 10 is 8" is a fundamental percentage problem. Understanding the various methods to solve this seemingly simple question lays a solid foundation for tackling more complex percentage calculations encountered in various aspects of life. By mastering these techniques and applying them to real-world scenarios, you can enhance your numerical skills and gain a deeper understanding of the ubiquitous role percentages play in our daily lives and across numerous fields. Remember, consistent practice and a clear grasp of the underlying principles are key to success in mastering percentage calculations.
Latest Posts
Latest Posts
-
How Many Degrees Are In A Half Circle
May 09, 2025
-
What Force Keeps The Planets In Orbit Around The Sun
May 09, 2025
-
What Are The Products Of This Chemical Reaction
May 09, 2025
-
What Are Some Examples Of A Screw
May 09, 2025
-
What Planet Is Known As The Morning Star
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 10 Is 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.