What Percent Is 3 Out Of 8
Juapaving
May 09, 2025 · 5 min read
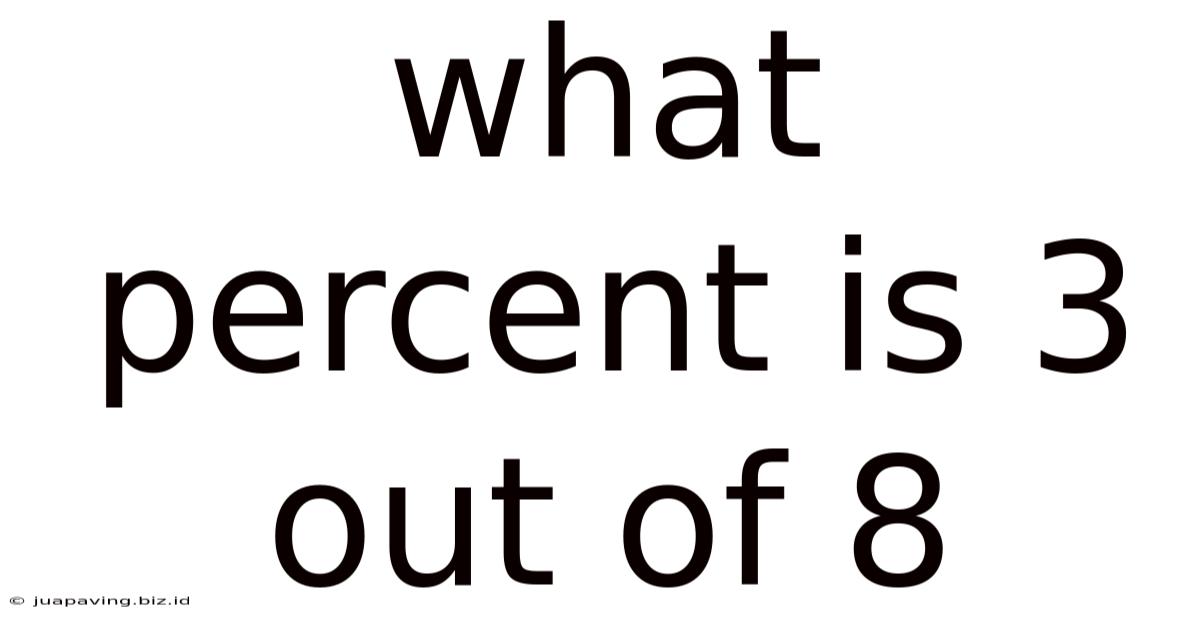
Table of Contents
What Percent is 3 Out of 8? A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article will delve into the question, "What percent is 3 out of 8?", providing not only the answer but also a comprehensive explanation of the underlying process, alternative methods of calculation, and practical applications of percentage calculations.
Understanding the Fundamentals: Fractions, Decimals, and Percentages
Before diving into the specific problem, let's solidify our understanding of the core concepts: fractions, decimals, and percentages. They are all different ways of representing parts of a whole.
-
Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, 3/8 represents three parts out of a total of eight parts.
-
Decimal: A decimal represents a part of a whole using a base-ten system. Decimals are expressed using a decimal point to separate the whole number part from the fractional part. For instance, 0.375 is a decimal representation of a fraction.
-
Percentage: A percentage represents a part of a whole as a fraction of 100. The percentage symbol (%) indicates that the number is a fraction of 100. For example, 37.5% means 37.5 parts out of 100 parts.
These three forms are interchangeable; you can convert one form into another. This inter-conversion is crucial for solving percentage problems.
Calculating "What Percent is 3 Out of 8?" - The Method
The question "What percent is 3 out of 8?" essentially asks us to convert the fraction 3/8 into a percentage. Here's how we do it:
-
Convert the Fraction to a Decimal: To convert a fraction to a decimal, divide the numerator by the denominator. In this case:
3 ÷ 8 = 0.375
-
Convert the Decimal to a Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%).
0.375 × 100 = 37.5%
Therefore, 3 out of 8 is 37.5%.
Alternative Methods: Using Proportions
Another effective approach to solving this type of problem involves using proportions. A proportion is an equation stating that two ratios are equal. We can set up a proportion to find the percentage:
-
Let 'x' represent the percentage we're trying to find.
-
We can set up the proportion: 3/8 = x/100
-
Cross-multiply: 8x = 300
-
Solve for x: x = 300/8 = 37.5
Therefore, using the proportion method, we again arrive at the answer: 3 out of 8 is 37.5%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in various real-world scenarios. Here are some examples:
-
Calculating Discounts: If a store offers a 20% discount on an item priced at $100, the discount amount is 20% of $100, which is $20. The final price would be $80.
-
Determining Tax Amounts: Sales tax is often calculated as a percentage of the purchase price. If the sales tax is 6% and you buy an item for $50, the tax amount is 6% of $50, which is $3. The total cost would be $53.
-
Analyzing Data: Percentages are commonly used to represent data in charts and graphs, making it easier to visualize and understand trends and comparisons. For example, if 60% of respondents in a survey preferred a certain product, it clearly illustrates the preference level.
-
Calculating Interest: Interest on loans and investments is often expressed as a percentage. Understanding percentage calculations helps you determine the interest earned or paid over time.
-
Understanding Grade Percentages: In education, grades are often expressed as percentages. Knowing the percentage score helps students understand their performance relative to the total possible score.
Beyond the Basics: Working with More Complex Percentages
While the "3 out of 8" example is straightforward, percentage calculations can become more complex. Let's explore some scenarios:
-
Calculating Percentage Increase/Decrease: These calculations involve determining the percentage change between two values. For instance, if the price of an item increases from $50 to $60, the percentage increase is calculated as [(60-50)/50] x 100% = 20%.
-
Finding the Original Value: Sometimes, you know the percentage and the final value, but you need to find the original value. For example, if an item is on sale for $75 after a 25% discount, you can set up an equation to find the original price.
-
Working with Compound Percentages: Compound percentages involve applying a percentage change multiple times. This is common in financial calculations where interest is compounded periodically.
-
Understanding Percentage Points: It's crucial to distinguish between percentage points and percentage changes. A change from 10% to 15% is a 5 percentage point increase, but a 50% percentage increase.
Mastering Percentage Calculations: Tips and Tricks
-
Practice regularly: The more you practice, the more comfortable you'll become with various percentage calculation methods.
-
Use online calculators: Many online calculators can help you verify your calculations and learn different approaches.
-
Visualize the problem: Sometimes, visualizing the problem as a fraction or a diagram can help clarify the calculations.
-
Break down complex problems: Large, complex percentage problems can be broken down into smaller, more manageable steps.
-
Check your work: Always double-check your calculations to avoid errors.
Conclusion: The Power of Percentages
Understanding how to calculate percentages is a critical life skill. The ability to convert fractions to decimals and percentages, and vice-versa, opens up a world of problem-solving possibilities in various fields. From everyday shopping to complex financial analysis, mastering percentages empowers you to make informed decisions and navigate a data-driven world confidently. The seemingly simple question, "What percent is 3 out of 8?", serves as a gateway to unlocking a broader comprehension of this essential mathematical concept. By applying the methods outlined in this article, you can confidently tackle various percentage problems and confidently apply your knowledge in numerous real-world situations.
Latest Posts
Latest Posts
-
Two Million Two Hundred And Fifty Thousand In Numbers
May 09, 2025
-
Write The Number In Two Other Forms
May 09, 2025
-
Why Is Blood Pressure Measured In Millimeters Of Mercury
May 09, 2025
-
The Frequency Of A Sound Wave Is Determined By The
May 09, 2025
-
Chromatin Condenses Into Chromosomes And Spindles Begin To Form
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 3 Out Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.