What Percent Is 2/3 Of 100
Juapaving
May 09, 2025 · 4 min read
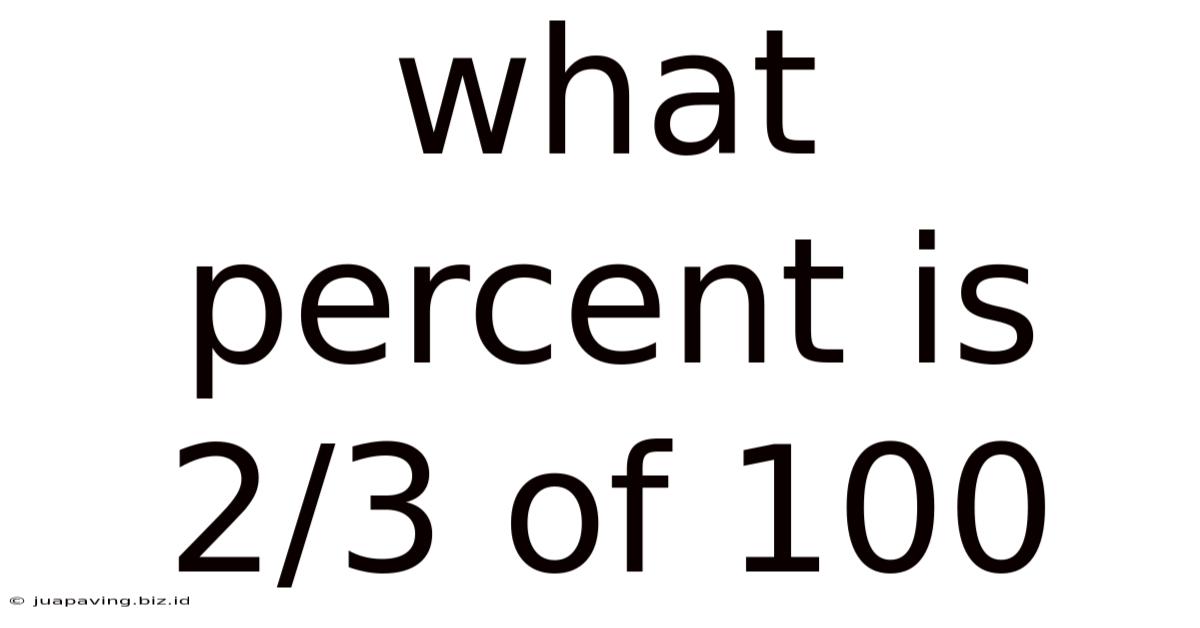
Table of Contents
What Percent is 2/3 of 100? A Deep Dive into Fractions, Percentages, and Conversions
This seemingly simple question, "What percent is 2/3 of 100?", opens a door to a broader understanding of fundamental mathematical concepts crucial for everyday life and advanced studies. This article will not only answer the question directly but also explore the underlying principles of fractions, percentages, and the vital conversions between them. We'll delve into practical applications and provide you with the tools to tackle similar problems with confidence.
Understanding Fractions and Percentages
Before jumping into the calculation, let's solidify our understanding of fractions and percentages.
Fractions: Representing Parts of a Whole
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into. For example, in the fraction 2/3, the numerator is 2, and the denominator is 3. This means we have 2 parts out of a total of 3 equal parts.
Percentages: Expressing Parts per Hundred
A percentage (%) represents a fraction where the denominator is always 100. It expresses a proportion relative to 100. For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Percentages are widely used to represent proportions, rates, and changes in various contexts, from finance to statistics.
Calculating 2/3 of 100
Now, let's tackle the main question: What percent is 2/3 of 100?
There are several ways to approach this calculation:
Method 1: Direct Calculation
- Find the fraction of 100: Multiply the fraction (2/3) by 100: (2/3) * 100 = 200/3
- Convert the improper fraction to a mixed number: 200/3 = 66 and 2/3
- Convert the mixed number to a percentage: 66 and 2/3 can be expressed as 66.666...% (repeating decimal). For practical purposes, we often round this to 66.67%.
Method 2: Using Decimal Equivalents
- Convert the fraction to a decimal: Divide the numerator (2) by the denominator (3): 2 ÷ 3 ≈ 0.6667
- Multiply the decimal by 100: 0.6667 * 100 ≈ 66.67%
Method 3: Proportions
We can set up a proportion to solve this:
2/3 = x/100
To solve for x (the percentage), cross-multiply:
3x = 200
x = 200/3 ≈ 66.67%
Understanding the Result: 66.67%
The answer, approximately 66.67%, signifies that 2/3 represents 66.67 parts out of 100. This is a recurring decimal, meaning the '67' continues infinitely. The slight rounding is a common practice for practical applications.
Practical Applications and Real-World Examples
The ability to convert fractions to percentages is vital in many real-world scenarios:
- Finance: Calculating interest rates, discounts, and profit margins. For example, a 2/3 discount on a $100 item means a discount of $66.67.
- Statistics: Representing data proportions, such as the percentage of students who passed an exam.
- Measurement and scaling: Converting fractional measurements to percentages for comparisons or scaling purposes.
- Everyday life: Calculating tips, sharing expenses, understanding sales, and more.
Beyond the Basics: Working with More Complex Fractions and Percentages
The principles discussed here extend to more complex scenarios. Let's consider some examples:
Example 1: Finding a percentage of a larger number:
What is 2/3 of 300?
Following the same methods:
(2/3) * 300 = 200
Therefore, 2/3 of 300 is 200, or (200/300)*100% = 66.67%.
Example 2: Calculating the original amount from a percentage:
If 66.67% of a number is 100, what is the original number?
Let x be the original number. We can set up the equation:
0.6667x = 100
x = 100 / 0.6667 ≈ 150
The original number is approximately 150.
Example 3: Working with different fractions:
What percentage is 3/8 of 200?
(3/8) * 200 = 75
75/200 * 100% = 37.5%
Mastering Fraction-to-Percentage Conversions: Tips and Tricks
- Memorize common fraction-decimal-percentage equivalents: Knowing these by heart will significantly speed up your calculations. For instance, 1/2 = 0.5 = 50%, 1/4 = 0.25 = 25%, 1/3 ≈ 0.3333 = 33.33%, 2/3 ≈ 0.6667 = 66.67%, etc.
- Practice regularly: The more you practice converting fractions to percentages, the more proficient you will become.
- Use a calculator: For more complex calculations, a calculator can save time and ensure accuracy.
- Understand the concept, not just the method: Focus on grasping the underlying mathematical principles rather than just memorizing formulas.
Conclusion: Embracing the Power of Fractions and Percentages
The seemingly simple question, "What percent is 2/3 of 100?" has led us on a journey exploring the fundamental concepts of fractions and percentages, their interrelationships, and their diverse applications in our daily lives. Mastering these concepts provides a powerful toolset for navigating various situations, from simple calculations to complex problem-solving across diverse fields. Remember, consistent practice and a solid understanding of the underlying principles are key to becoming proficient in these crucial mathematical skills. By understanding these principles, you can confidently tackle similar problems and apply these skills to real-world challenges.
Latest Posts
Latest Posts
-
Is 33 A Prime Number Or A Composite Number
May 10, 2025
-
Common Factors Of 48 And 64
May 10, 2025
-
Which Of The Following Mixtures Are Solutions
May 10, 2025
-
Difference Between Physical Capital And Human Capital
May 10, 2025
-
Cilia And Flagella Plant Or Animal Cell
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 2/3 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.