What Is The Unit Of Moment Of Inertia
Juapaving
Apr 04, 2025 · 6 min read
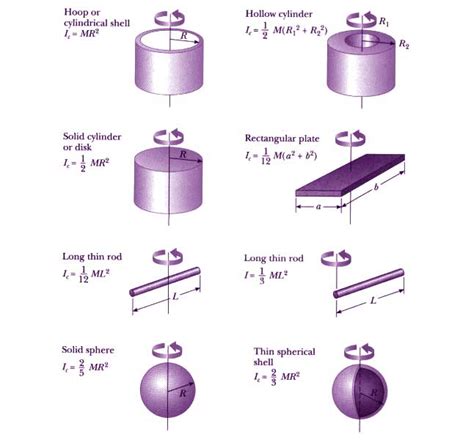
Table of Contents
What is the Unit of Moment of Inertia? A Comprehensive Guide
Moment of inertia, a crucial concept in physics and engineering, quantifies an object's resistance to changes in its rotation. Understanding its unit is fundamental to grasping its significance and applying it correctly in various calculations. This article delves deep into the definition, calculation, and the crucial aspect of the unit of moment of inertia. We'll explore different scenarios and provide practical examples to solidify your understanding.
Defining Moment of Inertia
Before we dive into the unit, let's establish a clear understanding of what moment of inertia actually represents. It's a measure of how difficult it is to change the rotational speed of a body. Think of it like the rotational equivalent of mass in linear motion. A larger mass requires a greater force to accelerate linearly; similarly, a larger moment of inertia requires a greater torque to accelerate rotationally.
The moment of inertia depends on two key factors:
- Mass: A greater mass inherently offers more resistance to changes in motion, both linear and rotational.
- Distribution of Mass: The way mass is distributed relative to the axis of rotation significantly impacts moment of inertia. Mass closer to the axis contributes less to the moment of inertia than mass farther away. A ring, for instance, has a higher moment of inertia than a solid disc of the same mass because its mass is concentrated farther from the axis.
Calculating Moment of Inertia
The mathematical representation of moment of inertia involves summing the product of each particle's mass and the square of its distance from the axis of rotation. For continuous bodies, this summation becomes an integral:
I = ∫ r² dm
Where:
- I represents the moment of inertia.
- r is the perpendicular distance of a mass element (dm) from the axis of rotation.
- dm is an infinitesimally small mass element.
The integral is taken over the entire body. The complexity of this integral depends heavily on the shape and mass distribution of the object. Standard formulas exist for common shapes like discs, spheres, rods, and cylinders, simplifying calculations considerably.
The Unit of Moment of Inertia: Kilogram-meter squared (kg⋅m²)
The unit of moment of inertia directly stems from its defining equation. Since mass (m) is measured in kilograms (kg) and distance (r) is measured in meters (m), the unit for moment of inertia (I) is kilogram-meter squared (kg⋅m²). This unit reflects the inherent properties of moment of inertia: it combines the mass of the object with the square of the distance from the axis of rotation. The squared distance emphasizes the disproportionate influence of mass farther from the axis.
Understanding the Unit's Significance
The kg⋅m² unit isn't just an arbitrary assignment; it carries significant physical meaning. It reflects the resistance to rotational acceleration. A larger kg⋅m² value implies a greater resistance to changes in rotational speed, requiring a larger torque to achieve the same angular acceleration. Conversely, a smaller kg⋅m² value indicates a lower resistance, allowing for easier rotational acceleration.
Moment of Inertia in Different Systems of Units
While kg⋅m² is the standard unit in the International System of Units (SI), other units might be used in different contexts:
- Pound-foot squared (lb⋅ft²): This is commonly used in the imperial system of units.
- Gram-centimeter squared (g⋅cm²): Occasionally encountered, especially in smaller-scale applications.
It's crucial to maintain consistency in units throughout any calculation involving moment of inertia to avoid errors. Conversion factors exist for switching between different unit systems.
Moment of Inertia and Rotational Kinetic Energy
The moment of inertia plays a vital role in calculating the rotational kinetic energy of a rotating body. Rotational kinetic energy is the energy an object possesses due to its rotation. The formula is:
KE<sub>rot</sub> = ½ Iω²
Where:
- KE<sub>rot</sub> is the rotational kinetic energy.
- I is the moment of inertia.
- ω is the angular velocity (radians per second).
Notice how the moment of inertia directly impacts the rotational kinetic energy. A larger moment of inertia, for a given angular velocity, results in higher rotational kinetic energy.
Parallel Axis Theorem: Shifting the Axis of Rotation
The parallel axis theorem provides a convenient method for calculating the moment of inertia of a body about an axis parallel to its center of mass. If you know the moment of inertia (I<sub>cm</sub>) about the center of mass and the distance (d) between the two parallel axes, the moment of inertia (I) about the new axis is:
I = I<sub>cm</sub> + Md²
Where:
- M is the total mass of the body.
This theorem is incredibly useful as it avoids the need for complex integration when dealing with axes not passing through the center of mass.
Radius of Gyration: A Simplified Representation
The radius of gyration (k) provides a simplified way to visualize the distribution of mass relative to the axis of rotation. It's defined as the distance from the axis of rotation at which the entire mass of the body could be concentrated to yield the same moment of inertia. The relationship is:
I = Mk²
Where:
- k is the radius of gyration.
This concept helps in understanding how the mass distribution affects the moment of inertia. A larger radius of gyration indicates that the mass is more spread out from the axis of rotation.
Applications of Moment of Inertia
The concept of moment of inertia isn't confined to theoretical physics; it finds widespread applications across various engineering disciplines:
1. Mechanical Engineering:
- Design of rotating machinery: Moment of inertia is crucial in designing flywheels, gears, turbines, and other rotating components. Proper consideration of moment of inertia ensures efficient energy transfer and minimizes vibrations.
- Vehicle dynamics: Understanding moment of inertia is vital in designing and analyzing vehicles, influencing stability, handling, and braking performance. The distribution of mass within a car directly impacts its yaw, pitch, and roll characteristics.
- Robotics: The moment of inertia of robot arms and links plays a key role in controlling their movements and optimizing energy consumption.
2. Aerospace Engineering:
- Aircraft design: Moment of inertia is essential for determining the stability and maneuverability of aircraft. The distribution of mass affects the aircraft's response to control inputs.
- Rocket design: The moment of inertia of a rocket influences its stability during launch and flight.
3. Civil Engineering:
- Structural dynamics: Moment of inertia is critical in analyzing the dynamic behavior of structures subjected to wind loads, earthquakes, or other dynamic forces. This helps engineers design structures that can withstand these forces without failure.
4. Physics:
- Classical mechanics: Moment of inertia is fundamental to understanding rotational motion, angular momentum, and torque.
- Quantum mechanics: The concept finds application in analyzing the rotational behavior of molecules and atoms.
Conclusion
The unit of moment of inertia, kilogram-meter squared (kg⋅m²), is not just a unit; it's a fundamental representation of an object's resistance to changes in its rotational motion. Understanding this unit, along with the concepts of mass distribution and the various methods for calculating moment of inertia, is crucial for anyone working with rotating systems. Its applications extend far beyond theoretical physics, impacting various engineering disciplines and playing a critical role in the design and analysis of a wide range of systems and structures. The thorough understanding of moment of inertia, its unit, and its applications ensures safer, more efficient, and robust designs across multiple sectors. From the smallest gears to the largest structures, the kg⋅m² unit stands as a testament to the power and practicality of this fundamental concept in physics and engineering.
Latest Posts
Latest Posts
-
Cam Plants Keep Stomata Closed In The Daytime
Apr 04, 2025
-
36 Inches Is How Many Centimeters
Apr 04, 2025
-
Five Letter Words Ending In O N
Apr 04, 2025
-
What Is Keratinization And Where Does It Occur
Apr 04, 2025
-
Drawing Of The Reaction Of Hydrochloric Acid With Water
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Unit Of Moment Of Inertia . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
