What Is The Tangent Of 30 Degrees
Juapaving
Apr 06, 2025 · 6 min read
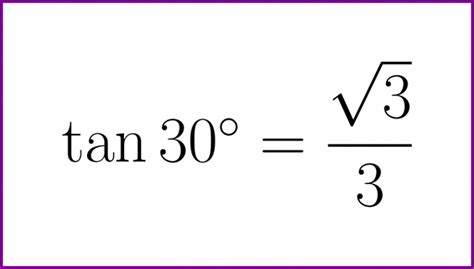
Table of Contents
What is the Tangent of 30 Degrees? A Deep Dive into Trigonometry
Trigonometry, the branch of mathematics dealing with the relationships between the sides and angles of triangles, is fundamental to many fields, from architecture and engineering to physics and computer graphics. A core concept within trigonometry is the tangent function, which relates the opposite and adjacent sides of a right-angled triangle. This article delves into the tangent of 30 degrees, exploring its value, derivation, applications, and significance within the broader context of trigonometry.
Understanding the Tangent Function
Before diving into the specifics of tan(30°), let's refresh our understanding of the tangent function. In a right-angled triangle, the tangent of an angle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. This can be expressed as:
tan(θ) = Opposite / Adjacent
where θ represents the angle in question.
This simple formula underpins a vast array of calculations and applications. The tangent function is particularly useful in determining unknown angles or sides in right-angled triangles, making it a cornerstone of surveying, navigation, and many other practical disciplines.
Deriving the Tangent of 30 Degrees
The value of tan(30°) can be derived using a 30-60-90 triangle, a special type of right-angled triangle with angles of 30°, 60°, and 90°. The ratio of the sides in a 30-60-90 triangle is always 1:√3:2.
Specifically:
- Shortest side (opposite 30°): 1
- Longer side (opposite 60°): √3
- Hypotenuse (opposite 90°): 2
Applying the tangent formula:
tan(30°) = Opposite / Adjacent = 1 / √3
To rationalize the denominator (a standard practice in mathematics to avoid irrational numbers in the denominator), we multiply both the numerator and denominator by √3:
tan(30°) = (1 * √3) / (√3 * √3) = √3 / 3
Therefore, the exact value of the tangent of 30 degrees is √3 / 3, which is approximately 0.57735.
Applications of tan(30°)
The value of tan(30°) finds numerous applications in various fields. Here are a few examples:
1. Surveying and Land Measurement:
Surveyors frequently use trigonometry to determine distances and elevations. Knowing the value of tan(30°) allows them to calculate the height of a structure or the distance across a body of water based on measurements of angles and known distances. For instance, if a surveyor measures a 30-degree angle of elevation to the top of a building from a known distance, they can readily compute the building's height using the tangent function.
2. Engineering and Construction:
In civil engineering and construction, the tangent function is crucial for designing ramps, slopes, and other inclined structures. Understanding the relationship between the angle of inclination and the slope ratio (rise over run) is essential for ensuring structural stability and safety. The 30-degree angle, with its corresponding tangent value, is often used in designing gentle slopes for accessibility.
3. Physics and Mechanics:
In physics, the tangent function is frequently employed in problems involving vectors, forces, and projectile motion. For example, calculating the angle of projection needed to achieve a specific range or determining the components of a force vector often requires the application of trigonometric functions, including the tangent. Understanding the value of tan(30°) helps simplify many such calculations.
4. Computer Graphics and Game Development:
In computer graphics and game development, trigonometric functions are fundamental for creating realistic 3D environments and animations. The tangent function plays a critical role in calculating transformations, rotations, and projections, enabling the generation of accurate and visually appealing graphics. The specific value of tan(30°) can be used to create precise 3D rotations and positioning.
5. Navigation and Aviation:
Navigation systems, including those used in aviation and marine applications, rely heavily on trigonometric calculations. Determining bearings, distances, and altitudes often involves the use of trigonometric functions like the tangent. Understanding the tangent of various angles, including 30 degrees, is essential for accurate navigation and course correction.
Understanding the Unit Circle and tan(30°)
The unit circle provides a visual representation of trigonometric functions. The unit circle is a circle with a radius of 1 centered at the origin of a coordinate plane. For any angle θ, the point where the terminal side of the angle intersects the unit circle has coordinates (cos θ, sin θ). The tangent of θ can then be found by calculating the ratio sin θ / cos θ.
For a 30-degree angle, the coordinates of the intersection point are (√3/2, 1/2). Therefore:
tan(30°) = sin(30°) / cos(30°) = (1/2) / (√3/2) = 1/√3 = √3/3
This reinforces the previously derived value of tan(30°). The unit circle offers a powerful visual tool for understanding the behavior of trigonometric functions and their interrelationships.
Beyond the Basics: Exploring Related Angles and Identities
Understanding tan(30°) provides a foundation for exploring other related angles and trigonometric identities.
Angles in other quadrants:
The tangent function is positive in the first and third quadrants and negative in the second and fourth quadrants. This means that the tangent of angles like 150°, 210°, and 330° (which are related to 30° through various symmetries) will have a value related to tan(30°), but may be positive or negative depending on the quadrant.
Trigonometric Identities:
Several trigonometric identities involve the tangent function and can be used to simplify expressions or solve equations. For instance, the relationship between tangent and cotangent (cot(θ) = 1/tan(θ)) is fundamental. Also, the identity tan(2θ) = 2tan(θ) / (1 - tan²(θ)) allows us to calculate the tangent of angles double the size of a known angle.
Practical Exercises and Problem Solving
To solidify your understanding of tan(30°), consider attempting these practical exercises:
-
Calculating Heights: A surveyor stands 100 meters from the base of a building and measures a 30-degree angle of elevation to the top of the building. Calculate the height of the building using tan(30°).
-
Ramp Design: An architect is designing a ramp with a 30-degree incline. If the horizontal distance covered by the ramp is 5 meters, calculate the vertical rise of the ramp.
-
Vector Resolution: A force vector of magnitude 10 Newtons is applied at a 30-degree angle to the horizontal. Calculate the horizontal and vertical components of this force vector using trigonometric functions.
These exercises demonstrate the practical application of tan(30°) in real-world scenarios, highlighting its importance across different disciplines.
Conclusion: The Significance of tan(30°) in Mathematics and Beyond
The tangent of 30 degrees, a seemingly simple concept in trigonometry, holds significant importance in various fields. Its precise value (√3/3) is not just a numerical result; it's a key element in numerous calculations and applications, from surveying and engineering to computer graphics and physics. Understanding its derivation, properties, and practical applications is essential for anyone pursuing studies or careers involving mathematics, engineering, science, or computer technology. Its foundational role in trigonometry highlights the interconnectedness of mathematical concepts and their impact on our understanding and manipulation of the physical world. Mastering this seemingly simple concept opens doors to a broader appreciation of the power and elegance of mathematics.
Latest Posts
Latest Posts
-
Simplify The Square Root Of 121
Apr 08, 2025
-
Adjective That Starts With N To Describe A Mom
Apr 08, 2025
-
How Do Humans And Other Consumers Obtain Nitrogen
Apr 08, 2025
-
1200 Square Feet To Square Meters
Apr 08, 2025
-
How To Find The Distance Between Two Parallel Lines
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Tangent Of 30 Degrees . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.