What Is The Sum Of The Angles Of A Hexagon
Juapaving
Mar 25, 2025 · 5 min read
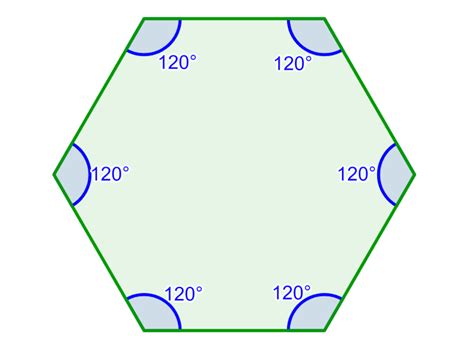
Table of Contents
What is the Sum of the Angles of a Hexagon? A Deep Dive into Geometry
The humble hexagon, a six-sided polygon, holds a fascinating secret within its geometric structure: the sum of its interior angles. While the answer itself is straightforward, understanding why that sum is what it is unlocks a deeper appreciation for geometric principles and their applications. This article delves into the fascinating world of hexagons, exploring the sum of their angles, different types of hexagons, and real-world examples. We'll also look at how to calculate the sum of angles in any polygon, regardless of the number of sides.
Understanding Polygons and Interior Angles
Before jumping into hexagons, let's establish a solid foundation. A polygon is any closed two-dimensional shape with straight sides. These sides can be of equal or unequal length, and the angles between them can also vary. Triangles (3 sides), quadrilaterals (4 sides), pentagons (5 sides), and hexagons (6 sides) are all examples of polygons.
The interior angles of a polygon are the angles formed inside the shape where two sides meet. It's these angles we're interested in summing. The sum of interior angles isn't a fixed number; it depends entirely on the number of sides the polygon has.
Deriving the Formula: Sum of Interior Angles of a Polygon
The key to finding the sum of the interior angles of any polygon lies in triangulation. We can divide any polygon into a series of triangles by drawing diagonals from a single vertex (corner) to all other non-adjacent vertices.
Consider a quadrilateral (4 sides). By drawing a single diagonal, we divide it into two triangles. Since each triangle has interior angles summing to 180°, the quadrilateral's total interior angle sum is 2 * 180° = 360°.
A pentagon (5 sides) can be divided into three triangles, resulting in an interior angle sum of 3 * 180° = 540°. A hexagon (6 sides) can be divided into four triangles, giving an interior angle sum of 4 * 180° = 720°.
Do you see the pattern? The number of triangles is always two less than the number of sides. This leads us to the general formula for the sum of interior angles (S) of an n-sided polygon:
S = (n - 2) * 180°
This formula is incredibly powerful because it works for any polygon, from a triangle (n=3) to a dodecagon (n=12) and beyond.
The Sum of Angles in a Hexagon: The Answer
Applying the formula to a hexagon (n=6), we get:
S = (6 - 2) * 180° = 4 * 180° = 720°
Therefore, the sum of the interior angles of any hexagon is 720 degrees. This holds true regardless of the hexagon's shape – whether it's a regular hexagon (with equal sides and angles) or an irregular hexagon (with unequal sides and angles).
Types of Hexagons: Regular vs. Irregular
While the sum of interior angles remains constant (720°), the individual angles within a hexagon can vary depending on its type:
Regular Hexagon
A regular hexagon has all six sides of equal length and all six angles of equal measure. Since the total sum is 720°, each interior angle of a regular hexagon measures 720° / 6 = 120°.
Irregular Hexagon
An irregular hexagon has sides and angles of varying lengths and measures. While the sum of its interior angles will always be 720°, the individual angles will differ. There's an infinite number of possible irregular hexagons, each with a unique combination of angles and side lengths.
Real-World Applications of Hexagons
Hexagons appear surprisingly often in the natural world and in human constructions:
-
Honeycombs: Bees construct their honeycombs using hexagonal cells, maximizing storage space while minimizing the amount of wax needed. The hexagonal shape's efficiency is a testament to nature's optimization strategies.
-
Snowflakes: Many snowflakes exhibit hexagonal symmetry, although the specific patterns are highly variable. The hexagonal structure arises from the crystalline structure of water molecules.
-
Graphite: The carbon atoms in graphite are arranged in a hexagonal lattice structure, contributing to its unique properties like conductivity.
-
Architecture and Design: Hexagons are employed in various architectural and design applications, including tiling patterns, structural elements, and even artistic creations. The pleasing aesthetic of hexagons makes them a popular choice for design.
-
Engineering: Hexagonal shapes can provide structural strength and stability in engineering designs, offering advantages in weight distribution and stress management.
Calculating Interior Angles of Irregular Hexagons
While the sum of the interior angles is always 720°, finding the measure of each individual angle in an irregular hexagon requires more information. You'll typically need to know the measurements of at least four angles to determine the remaining two angles using the known sum.
For example, if you know five angles of an irregular hexagon (let's say 110°, 125°, 130°, 105°, and 140°), you can find the sixth angle using the following equation:
720° - (110° + 125° + 130° + 105° + 140°) = x
Solving for x, we find that the missing angle measures 110°.
Beyond Hexagons: Exploring Other Polygons
The principle of triangulation and the formula (n - 2) * 180° applies to any polygon, allowing us to calculate the sum of its interior angles. This understanding extends our geometrical knowledge beyond just hexagons, revealing a unifying principle across all polygonal shapes. For instance:
- Heptagon (7 sides): (7 - 2) * 180° = 900°
- Octagon (8 sides): (8 - 2) * 180° = 1080°
- Nonagon (9 sides): (9 - 2) * 180° = 1260°
- Decagon (10 sides): (10 - 2) * 180° = 1440°
Conclusion: The Significance of the Hexagon's Angle Sum
The seemingly simple question of the sum of a hexagon's angles unveils a rich tapestry of geometric concepts. From the fundamental formula governing the interior angles of any polygon to the diverse applications of hexagons in nature and human endeavors, this exploration highlights the beauty and practicality of geometric principles. Understanding this fundamental concept lays a strong foundation for further exploration into more advanced geometry and its applications in various fields. The consistent 720° sum for all hexagons, regardless of shape, is a testament to the elegant and predictable nature of mathematics. This consistent rule underscores the importance of geometrical understanding in solving complex problems and appreciating the order underlying seemingly diverse shapes and patterns.
Latest Posts
Latest Posts
-
Is 9 A Multiple Of 3
Mar 28, 2025
-
Lcm Of 5 7 And 2
Mar 28, 2025
-
Barium Chloride Reacts With Sodium Sulfate
Mar 28, 2025
-
Tension Is Measured In What Units
Mar 28, 2025
-
What Is The Decimal For 7
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Is The Sum Of The Angles Of A Hexagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
