What Is The Square Root Of 39
Juapaving
Apr 07, 2025 · 5 min read
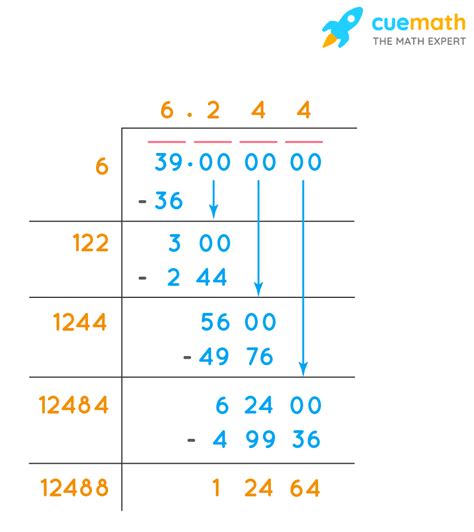
Table of Contents
What is the Square Root of 39? A Deep Dive into Irrational Numbers and Approximation Techniques
The seemingly simple question, "What is the square root of 39?", opens a door to a fascinating world of mathematics, encompassing irrational numbers, approximation methods, and the historical evolution of our understanding of numbers. While a precise, finite decimal representation doesn't exist, understanding how to approach this problem reveals much about the beauty and complexity of mathematics.
Understanding Square Roots
Before delving into the specifics of the square root of 39, let's establish a foundational understanding. The square root of a number, denoted as √x, is a value that, when multiplied by itself, equals x. For example, the square root of 9 (√9) is 3 because 3 * 3 = 9. This concept is fundamental in various mathematical fields, from geometry (calculating the sides of squares and other shapes) to algebra and calculus.
Why the Square Root of 39 is Irrational
Unlike the square root of 9 or 16, which yield whole numbers, the square root of 39 is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation is non-repeating and non-terminating; it goes on forever without showing any pattern. This characteristic distinguishes it from rational numbers, such as 0.5 (1/2) or 0.333... (1/3), which have either terminating or repeating decimal expansions.
The proof of the irrationality of √39 relies on a method similar to the proof by contradiction often used for demonstrating the irrationality of √2. Assuming √39 is rational, we can express it as a/b, where a and b are integers with no common factors (meaning the fraction is simplified). Squaring both sides gives 39 = a²/b². Rearranging, we have 39b² = a². This means a² is divisible by 39. Since 39 = 3 x 13, it implies a is divisible by both 3 and 13, and therefore divisible by 39. We can rewrite a as 39k (where k is an integer). Substituting this into the equation, we get 39b² = (39k)² = 1521k². Dividing both sides by 39, we find b² = 39k². This shows that b² is also divisible by 39, meaning b is divisible by 39. However, this contradicts our initial assumption that a and b have no common factors. This contradiction proves that √39 must be irrational.
Approximating the Square Root of 39
Since we cannot express √39 exactly as a decimal, we rely on approximation techniques. Several methods exist, each with varying levels of accuracy and complexity:
1. Using a Calculator
The simplest method is to use a calculator. Most scientific calculators have a square root function (√) that provides a reasonably accurate approximation. A calculator will usually display something like 6.244997998...
2. The Babylonian Method (or Heron's Method)
This iterative method offers a powerful way to approximate square roots with increasing accuracy. It works by repeatedly refining an initial guess. The formula is:
x_(n+1) = (x_n + S/x_n) / 2
Where:
- x_n is the current approximation
- x_(n+1) is the next (improved) approximation
- S is the number whose square root we're seeking (in our case, 39)
Let's illustrate with an initial guess of x_0 = 6:
- x_1 = (6 + 39/6) / 2 ≈ 6.25
- x_2 = (6.25 + 39/6.25) / 2 ≈ 6.24499
- x_3 = (6.24499 + 39/6.24499) / 2 ≈ 6.244997998
As you can see, with each iteration, the approximation gets closer to the actual value.
3. Linear Approximation
A simpler, though less accurate, method involves using a linear approximation. This leverages the fact that the square root function is relatively smooth. We can use the derivative to estimate the change in the square root based on a known value. For example, we know √36 = 6. Since 39 is close to 36, we can estimate:
√39 ≈ √36 + (39 - 36) * (1/(2√36)) ≈ 6 + 3 * (1/12) ≈ 6.25
This method provides a quick, rough estimate but lacks the precision of the Babylonian method.
4. Using Continued Fractions
Continued fractions provide another way to represent irrational numbers. While calculating the continued fraction for √39 is more complex than other methods, it offers a unique representation that converges towards the exact value. The continued fraction for √39 starts as follows:
6 + 1/(12 + 1/(12 + 1/(12 + ...)))
Applications of the Square Root of 39
While the square root of 39 might seem like an abstract mathematical concept, it has practical applications in various fields:
- Physics: Calculations involving vectors and velocities often involve square roots.
- Engineering: Designing structures and calculating forces might utilize square root calculations.
- Computer Graphics: Generating realistic images and animations requires extensive mathematical computations, including square roots.
- Finance: Calculating investment returns sometimes involves applying square root operations.
- Geometry: Determining the lengths of diagonals in certain shapes will require calculating square roots.
The Historical Significance of Irrational Numbers
The discovery of irrational numbers like √39 significantly impacted the development of mathematics. The ancient Greeks, who primarily worked with rational numbers, were initially baffled by the existence of numbers that couldn't be represented as fractions. This discovery challenged their understanding of number systems and contributed to the evolution of more sophisticated mathematical frameworks.
Conclusion: Embracing the Inexact
The square root of 39, while an irrational number with an infinite, non-repeating decimal expansion, is a perfect example of the beauty and complexity of mathematics. While we cannot write down its exact value, understanding the different approximation methods highlights the power of mathematical tools and allows us to work effectively with irrational numbers in various applications. The journey of approximating √39 serves as a valuable lesson in the practical application of mathematical principles and the enduring quest for precision and understanding. The ongoing exploration and development of advanced computational techniques further demonstrate humanity's continuous effort to refine our understanding and manipulation of such fascinating numbers. The seemingly simple question, "What is the square root of 39?", unlocks a rich tapestry of mathematical concepts and historical context, highlighting the endless fascination and continuous exploration within the realm of mathematics.
Latest Posts
Latest Posts
-
What Is Standard Form Of A Polynomial
Apr 08, 2025
-
Which Pair Of Triangles Is Similar
Apr 08, 2025
-
Least Common Multiple Of 11 And 10
Apr 08, 2025
-
Which Pair Of Triangles Are Congruent By Asa
Apr 08, 2025
-
What Is The Lcm Of 40 And 15
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 39 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.