What Is The Square Root Of 300
Juapaving
Mar 25, 2025 · 5 min read
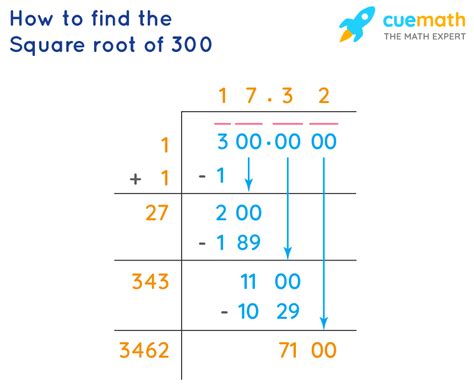
Table of Contents
What is the Square Root of 300? A Deep Dive into Square Roots and Approximation Techniques
The question, "What is the square root of 300?" seems simple enough. However, exploring this seemingly straightforward mathematical concept opens doors to a fascinating world of numerical approximation, algorithm design, and the historical development of mathematical understanding. This article will not only answer the question directly but also delve into the methods used to calculate square roots, discuss their applications, and explore the underlying mathematical principles.
Understanding Square Roots
Before we tackle the square root of 300, let's establish a solid understanding of what a square root is. The square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3, because 3 * 3 = 9. We denote the square root using the radical symbol √.
Symbolically, if x² = y, then √y = x. This simple definition lays the groundwork for understanding more complex calculations.
Calculating the Square Root of 300: The Exact Value
Unfortunately, the square root of 300 isn't a whole number or a simple fraction. It's an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating. Therefore, we can only find an approximation.
Using a calculator, we find that the square root of 300 is approximately 17.3205081. This is a decimal approximation, and its precision depends on the calculator's capabilities.
Methods for Approximating Square Roots
Throughout history, mathematicians have developed various methods to approximate square roots. Let's explore a few:
1. Prime Factorization and Simplification
The first step in approximating any square root is to simplify the number under the radical sign using prime factorization. This involves breaking down the number into its prime factors.
300 = 2 x 2 x 3 x 5 x 5 = 2² x 3 x 5²
Notice that we have a perfect square, 2² and 5². We can simplify the expression as follows:
√300 = √(2² x 3 x 5²) = √2² x √3 x √5² = 2 x 5 x √3 = 10√3
This simplifies the calculation, as we now only need to approximate the square root of 3, which is approximately 1.732. Therefore:
10√3 ≈ 10 x 1.732 = 17.32
This method provides a reasonable approximation, especially when dealing with larger numbers.
2. The Babylonian Method (or Heron's Method)
This iterative method is an ancient algorithm that refines an initial guess to achieve greater accuracy. It works as follows:
-
Start with an initial guess: Let's start with 17, as we know the square root of 300 is slightly above 17.
-
Improve the guess: Divide the number (300) by the initial guess (17), and then average the result with the initial guess:
(17 + 300/17) / 2 ≈ 17.3235
-
Repeat step 2: Use the result from step 2 as the new guess and repeat the process. The more iterations you perform, the closer you get to the actual square root. Let's do one more iteration:
(17.3235 + 300/17.3235) / 2 ≈ 17.3205
As you can see, with just two iterations, we get a very close approximation to the value obtained using a calculator.
3. Newton-Raphson Method
This is a more sophisticated iterative method that converges faster than the Babylonian method. It relies on calculus and uses the derivative of the function to refine the approximation. While the explanation requires calculus knowledge and would be too complex for this general audience, it's worth noting that the Newton-Raphson method is a powerful tool for approximating square roots and other complex mathematical functions.
Applications of Square Roots
Understanding and calculating square roots is fundamental to various fields, including:
-
Physics: Calculating distances, velocities, and accelerations often involve square roots. For example, the Pythagorean theorem (a² + b² = c²) is used extensively in physics and requires calculating square roots to find the hypotenuse.
-
Engineering: Square roots are essential in structural engineering, electrical engineering, and many other engineering disciplines for solving equations and modeling systems.
-
Computer Graphics: Rendering 2D and 3D graphics often uses square roots for calculations involving distances, rotations, and transformations.
-
Finance: Calculating standard deviation and variance in financial data involves square roots.
-
Statistics: Square roots are used in numerous statistical calculations, including standard error and confidence intervals.
Beyond the Square Root of 300: Exploring Further
While we have focused on the square root of 300, the concepts and methods discussed are applicable to calculating the square root of any non-negative number. Further exploration could involve:
-
Higher-order roots: Investigating cube roots (∛), fourth roots (∜), and other higher-order roots.
-
Complex numbers: Exploring the square roots of negative numbers, which leads to the concept of imaginary and complex numbers.
-
Numerical analysis: Delving deeper into the algorithms and techniques used for approximating square roots and other mathematical functions.
Conclusion
The seemingly simple question of "What is the square root of 300?" opens a window into a rich and fascinating area of mathematics. From ancient approximation techniques to sophisticated algorithms, the pursuit of accurate calculations has driven mathematical progress for centuries. Understanding square roots is fundamental to numerous fields, and the methods discussed in this article provide valuable insights into their calculation and practical applications. Whether you're a student grappling with basic mathematics or a professional using these concepts in your work, grasping the essence of square roots is a key step in understanding the power and beauty of mathematics. Remember, the beauty of mathematics lies not just in the answer but in the journey of discovery and understanding the underlying processes.
Latest Posts
Latest Posts
-
In The Periodic Table Horizontal Rows Are Called
Mar 28, 2025
-
Why Does The Pupil Of The Eye Appear Black
Mar 28, 2025
-
Is 9 A Multiple Of 3
Mar 28, 2025
-
Lcm Of 5 7 And 2
Mar 28, 2025
-
Barium Chloride Reacts With Sodium Sulfate
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
