What Is The Percentage Of 6/5
Juapaving
May 09, 2025 · 4 min read
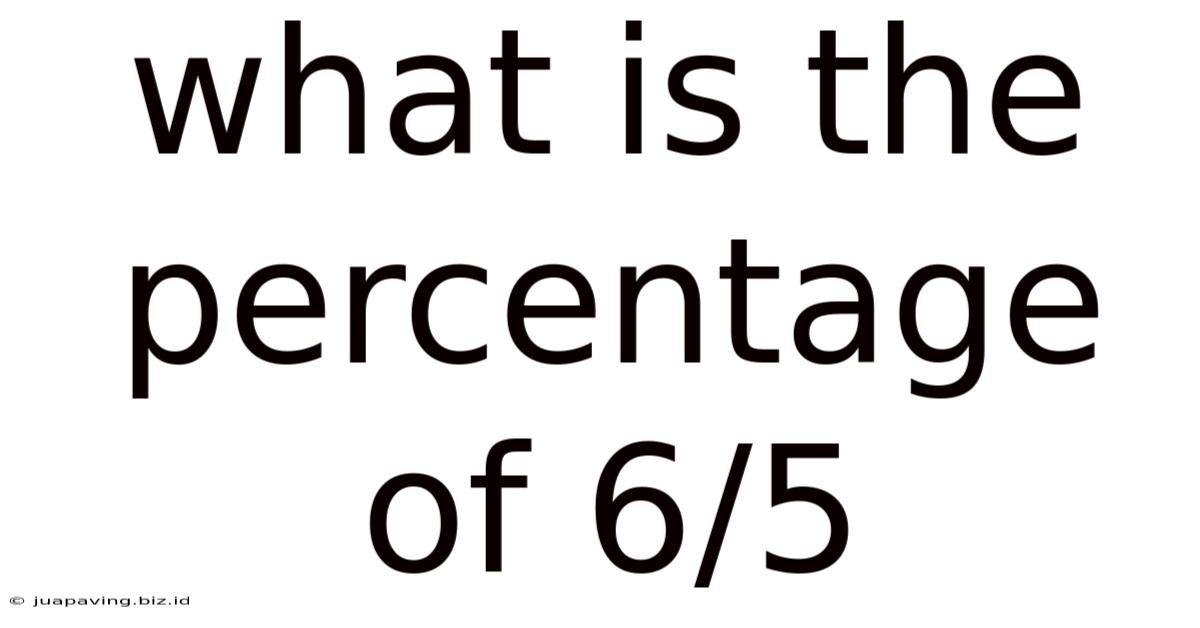
Table of Contents
What is the Percentage of 6/5? Understanding Fractions and Percentages
The question "What is the percentage of 6/5?" might seem simple at first glance, but it unlocks a crucial understanding of how fractions and percentages relate. This article will delve into the calculation, explore the underlying concepts, and offer practical applications to solidify your grasp of this fundamental mathematical principle.
Understanding Fractions and Percentages
Before diving into the calculation, let's establish a clear understanding of fractions and percentages.
What is a Fraction?
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts the whole is divided into. For example, in the fraction 6/5, 6 is the numerator and 5 is the denominator. This means we have 6 parts out of a total of 5 parts. Note that this is an improper fraction, where the numerator is larger than the denominator.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per hundred". For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are widely used to express proportions, rates, and changes in various contexts, from financial markets to scientific measurements.
Calculating the Percentage of 6/5
To convert the fraction 6/5 into a percentage, we need to follow these steps:
-
Convert the fraction to a decimal: Divide the numerator (6) by the denominator (5). 6 ÷ 5 = 1.2
-
Multiply the decimal by 100: This converts the decimal to a percentage. 1.2 × 100 = 120
-
Add the percentage symbol: This indicates that the result is a percentage. 120%
Therefore, 6/5 is equal to 120%.
Interpreting the Result: More Than 100%
The result, 120%, might seem unusual at first. Most people are accustomed to percentages ranging from 0% to 100%. However, percentages can exceed 100% when the part is larger than the whole. In the case of 6/5, we have more than the initial whole (5 parts). Think of it like this:
- Imagine you have a pizza cut into 5 slices.
- You eat 6 slices.
- You've eaten more than the whole pizza. This is represented by the 120%.
This illustrates that percentages aren't limited to the 0-100% range. They can represent values greater than the whole, indicating an increase or growth exceeding the original amount.
Practical Applications of Percentages Exceeding 100%
Percentages exceeding 100% find application in various real-world scenarios:
- Financial Growth: If a company's profits increase by 150% from the previous year, it means its profits have more than doubled.
- Population Increase: If a city's population grows by 110% over a decade, it means the population has increased by more than its initial size.
- Production Efficiency: If a factory's production output exceeds its target by 125%, it signifies significant improvement in efficiency.
- Data Analysis: In statistical analysis, percentage changes above 100% can indicate significant increases or deviations from the norm.
Beyond the Basics: Further Exploration of Fractions and Percentages
Understanding fractions and percentages is a foundation for more advanced mathematical concepts. Here are some related areas to explore:
Working with Mixed Numbers:
The fraction 6/5 can also be expressed as a mixed number: 1 1/5. This represents one whole and one-fifth. Converting mixed numbers to percentages involves similar steps:
- Convert the mixed number to an improper fraction: 1 1/5 becomes (1 * 5 + 1)/5 = 6/5
- Follow the steps outlined earlier to convert the improper fraction to a percentage.
Dealing with Different Denominators:
When working with different fractions, it's often necessary to find a common denominator before comparing them or converting them to percentages.
Percentage Increase and Decrease Calculations:
Understanding percentage changes is vital in numerous contexts. For instance, calculating a percentage increase involves determining the difference between two values, dividing it by the original value, and multiplying by 100.
Advanced Percentage Applications: Compound Interest, Growth Rates, and more:
As you progress in your mathematical journey, you'll encounter more complex applications of percentages, like compound interest calculations, exponential growth models, and various statistical analyses that rely heavily on proportional relationships.
Conclusion: Mastering Fractions and Percentages
The simple question of "What is the percentage of 6/5?" has led us on a journey through the fundamental concepts of fractions and percentages. We discovered that 6/5 represents 120%, emphasizing that percentages can and do exceed 100%. Understanding these concepts, their interconnectedness, and their diverse applications is essential for success in various academic and professional fields. This understanding builds a strong foundation for tackling more advanced mathematical problems and interpreting data effectively in real-world scenarios. Remember that mastering these basic mathematical concepts is key to building a strong numerical literacy foundation for more complex endeavors.
Latest Posts
Latest Posts
-
What Does A Tape Diagram Look Like
May 09, 2025
-
Is Coffee A Base Or An Acid
May 09, 2025
-
What Are The Inside Angles Of A Hexagon
May 09, 2025
-
Weathering And Erosion Compare And Contrast
May 09, 2025
-
What Is 3 Percent Of 150000
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 6/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.