What Is The Percentage Of 17 Out Of 25
Juapaving
May 14, 2025 · 5 min read
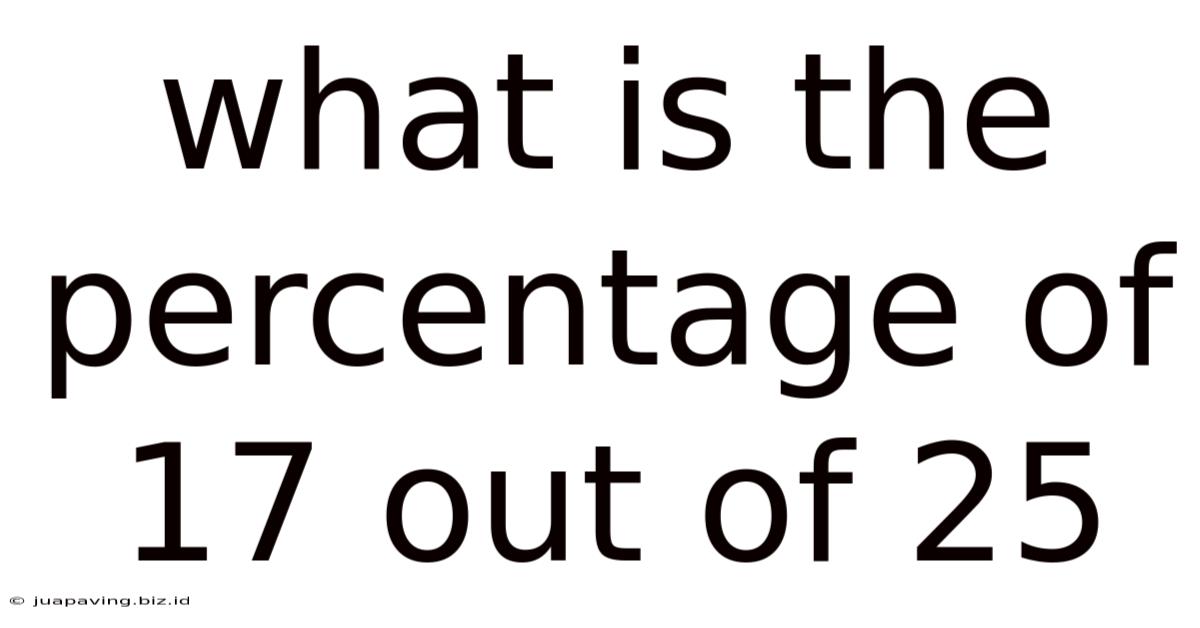
Table of Contents
What is the Percentage of 17 out of 25? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from academic studies and financial management to everyday decision-making. Understanding how to calculate percentages efficiently and accurately is crucial for navigating numerous situations. This comprehensive guide delves into the specifics of calculating the percentage of 17 out of 25, offering a step-by-step approach, practical examples, and exploring broader applications of percentage calculations.
Understanding Percentages: The Basics
Before we dive into calculating the percentage of 17 out of 25, let's review the fundamental concept of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "out of 100" or "per hundred." Essentially, a percentage expresses a proportion of a whole.
Key Terminology:
- Part: The specific portion of the whole you are considering (in our case, 17).
- Whole: The total amount or the complete quantity (in our case, 25).
- Percentage: The proportional representation of the part relative to the whole, expressed as a number out of 100.
Calculating the Percentage of 17 out of 25: Step-by-Step Guide
There are several ways to calculate the percentage of 17 out of 25. Let's explore two common methods:
Method 1: Using the Formula
The most straightforward method involves using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part = 17
- Whole = 25
Substituting these values into the formula:
(17 / 25) x 100% = 68%
Therefore, 17 out of 25 is 68%.
Method 2: Converting to a Decimal and then to a Percentage
This method involves first converting the fraction 17/25 into a decimal and then multiplying by 100 to express it as a percentage.
-
Convert the fraction to a decimal: 17 divided by 25 equals 0.68
-
Multiply the decimal by 100 to get the percentage: 0.68 x 100% = 68%
Again, we arrive at the same answer: 68%.
Practical Applications of Percentage Calculations
Percentage calculations are incredibly versatile and find applications across numerous fields. Here are some examples:
1. Academic Performance:
Imagine a student scored 17 out of 25 on a quiz. Using the percentage calculation, we determine their score is 68%, providing a clear representation of their performance relative to the total possible marks. This allows for easy comparison with other students and assessments.
2. Financial Calculations:
Percentages are fundamental in finance. For example, calculating interest rates, discounts, tax rates, profit margins, and investment returns all rely on percentage calculations. If a product is discounted by 20%, and its original price is $50, the discount would be 20% of $50, calculated as (20/100) x $50 = $10, resulting in a final price of $40.
3. Data Analysis and Statistics:
In data analysis and statistics, percentages are crucial for representing proportions within datasets. For instance, if a survey of 25 people shows 17 prefer a particular brand, the percentage (68%) provides a clear picture of brand preference within the sample population. This information is valuable for market research and product development.
4. Everyday Life:
Percentages are frequently encountered in everyday situations, such as calculating tips in restaurants (e.g., a 15% tip on a $20 meal), understanding sales tax rates, figuring out discounts at stores, and comprehending nutritional information on food labels (e.g., percentage of daily value for various nutrients).
Beyond the Basics: Advanced Percentage Calculations
While calculating the percentage of 17 out of 25 is a relatively straightforward task, there are more complex scenarios involving percentages:
1. Finding the Part when the Percentage and Whole are Known:
If we know that 68% of a total amount is 17, and we want to find the total amount (the whole), we can use the formula:
Part / (Percentage/100) = Whole
17 / (68/100) = 25
2. Finding the Percentage Increase or Decrease:
Percentage changes are essential for tracking trends and growth. For example, if the price of an item increases from $20 to $25, the percentage increase is calculated as:
((New Value - Old Value) / Old Value) x 100%
((25 - 20) / 20) x 100% = 25%
3. Compound Interest Calculations:
Compound interest involves earning interest on both the principal amount and accumulated interest. The formula for compound interest calculations utilizes percentages to determine the growth of an investment over time. This is a more complex application of percentages used in financial planning and investments.
Mastering Percentages: Tips and Tricks
Here are some tips to improve your proficiency with percentage calculations:
-
Memorize common fractions and their percentage equivalents: Familiarizing yourself with common fractions like 1/2 (50%), 1/4 (25%), 1/5 (20%), etc., will greatly speed up your calculations.
-
Utilize online calculators and tools: Numerous online calculators are available to simplify percentage calculations, particularly for more complex scenarios.
-
Practice regularly: The key to mastering percentage calculations is consistent practice. Work through various examples and problems to build your understanding and confidence.
-
Understand the underlying concepts: Instead of just memorizing formulas, make sure you grasp the core concepts of percentages, fractions, and ratios. This deeper understanding will enable you to tackle more challenging problems.
Conclusion: The Power of Percentage Calculations
Calculating the percentage of 17 out of 25, as we've demonstrated, is a fundamental skill with far-reaching implications. This guide provided a detailed explanation of the calculation process, explored various methods, and highlighted the broad applications of percentage calculations in academic pursuits, finance, data analysis, and everyday life. By mastering percentage calculations and understanding the underlying principles, individuals can enhance their problem-solving capabilities and navigate various quantitative challenges with greater efficiency and accuracy. The ability to swiftly and accurately calculate percentages is a valuable asset in numerous aspects of life, empowering individuals to make informed decisions and interpret data effectively.
Latest Posts
Latest Posts
-
Number In Words From 1 To 100
May 14, 2025
-
What Is 96 Inches In Feet
May 14, 2025
-
What Percentage Is 35 Out Of 40
May 14, 2025
-
Electricity Is Measured In What Unit
May 14, 2025
-
Is A Pencil A Conductor Or Insulator
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 17 Out Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.