What Is The Lowest Common Multiple Of 16 And 24
Juapaving
Apr 15, 2025 · 5 min read
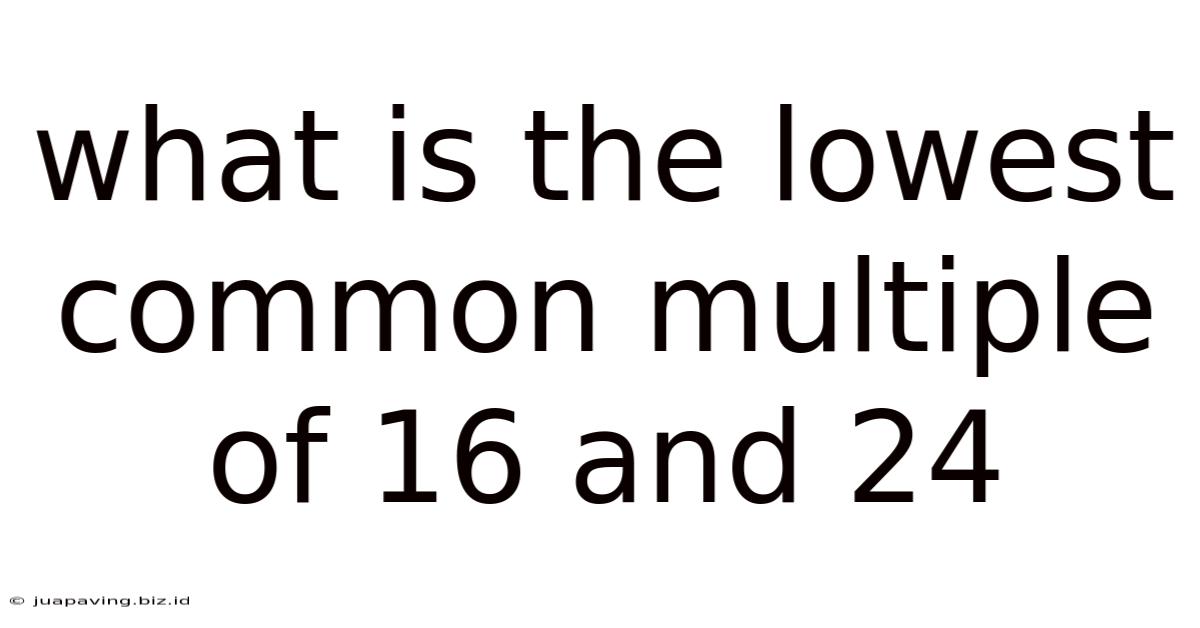
Table of Contents
What is the Lowest Common Multiple (LCM) of 16 and 24? A Deep Dive into Finding LCMs
Finding the lowest common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it can be surprisingly insightful. This article delves deep into determining the LCM of 16 and 24, exploring various approaches and highlighting the broader significance of LCMs in mathematics and beyond. We'll also touch upon the relationship between LCM and the greatest common divisor (GCD), offering a comprehensive understanding of these fundamental mathematical concepts.
Understanding Lowest Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 16 and 24, let's establish a solid understanding of what an LCM actually is. The lowest common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly.
Why are LCMs important? LCMs have practical applications in various areas, including:
- Fraction Arithmetic: Finding a common denominator when adding or subtracting fractions.
- Scheduling Problems: Determining when events will occur simultaneously (e.g., two buses arriving at the same stop).
- Music Theory: Calculating the frequency of rhythmic patterns.
- Engineering: Coordinating cyclical processes in machinery.
Method 1: Listing Multiples
One of the simplest methods to find the LCM is by listing the multiples of each number until a common multiple is found. Let's apply this to 16 and 24:
Multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160...
Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, 240...
By comparing the lists, we can see that the smallest common multiple is 48. Therefore, the LCM(16, 24) = 48.
While this method works well for smaller numbers, it becomes less efficient as the numbers get larger. Finding the LCM of, say, 144 and 288 through this method would require listing a significant number of multiples.
Method 2: Prime Factorization
A more efficient and systematic approach involves using prime factorization. This method is particularly useful for larger numbers. Let's break down 16 and 24 into their prime factors:
- 16 = 2 x 2 x 2 x 2 = 2⁴
- 24 = 2 x 2 x 2 x 3 = 2³ x 3
To find the LCM using prime factorization:
- Identify the prime factors: The prime factors involved are 2 and 3.
- Find the highest power of each prime factor: The highest power of 2 is 2⁴ (from 16), and the highest power of 3 is 3¹ (from 24).
- Multiply the highest powers: LCM(16, 24) = 2⁴ x 3¹ = 16 x 3 = 48
This method provides a concise and reliable way to calculate the LCM, regardless of the size of the numbers involved.
Method 3: Using the GCD (Greatest Common Divisor)
The LCM and GCD are closely related. There's a formula that links them:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two integers.
First, let's find the GCD of 16 and 24 using the Euclidean Algorithm:
- Divide the larger number (24) by the smaller number (16): 24 ÷ 16 = 1 with a remainder of 8.
- Replace the larger number with the smaller number (16) and the smaller number with the remainder (8): 16 ÷ 8 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 8. Therefore, GCD(16, 24) = 8.
Now, we can use the formula:
LCM(16, 24) x GCD(16, 24) = 16 x 24 LCM(16, 24) x 8 = 384 LCM(16, 24) = 384 ÷ 8 = 48
Comparing the Methods
All three methods – listing multiples, prime factorization, and using the GCD – arrive at the same answer: the LCM of 16 and 24 is 48. However, the efficiency of each method varies:
- Listing Multiples: Simple for small numbers but becomes impractical for larger numbers.
- Prime Factorization: Efficient and systematic, works well for both small and large numbers.
- Using the GCD: Requires calculating the GCD first, but provides a direct formula to compute the LCM. This method is generally efficient, especially when dealing with larger numbers where finding the prime factors might be computationally expensive.
LCM in Real-World Applications
The concept of LCM isn't confined to theoretical mathematics. It has practical applications in many areas:
- Construction: In tiling or bricklaying, the LCM helps determine the optimal spacing to ensure patterns align perfectly.
- Scheduling: Coordinating work schedules, transportation routes, or machine cycles to minimize downtime.
- Music: Determining when different musical phrases or rhythms will align.
- Cooking: Measuring ingredients precisely when recipes require different fractional amounts.
Understanding LCMs allows us to solve problems involving cycles, patterns, and synchronization, which makes it a valuable tool in various fields.
Beyond Two Numbers: Finding the LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you simply consider all prime factors and their highest powers across all numbers. For the GCD method, you would need to find the GCD of all numbers iteratively and then use a generalized formula. Listing multiples becomes even more inefficient with multiple numbers.
Conclusion: Mastering LCM Calculations
Finding the lowest common multiple is a fundamental mathematical skill with far-reaching applications. While the simplest method of listing multiples works for small numbers, prime factorization and the GCD method offer more efficient and reliable approaches, particularly when dealing with larger integers. Understanding these different methods empowers you to solve various real-world problems involving cycles, timing, and synchronization. Remember, the key to mastering LCM calculations lies in understanding the underlying concepts and choosing the most efficient method for the problem at hand. Through practice and understanding, calculating LCMs becomes a straightforward and essential tool in your mathematical toolkit. And, as we've demonstrated, the LCM of 16 and 24 is definitively 48.
Latest Posts
Latest Posts
-
Cuanto Es 14 Inches En Centimetros
May 10, 2025
-
Objects That Start With Letter X
May 10, 2025
-
At What Height Above The Surface Of Earth
May 10, 2025
-
How Does Binary Fission Differ From Mitosis
May 10, 2025
-
Sum Of The Kinetic Energy And Potential Energy
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lowest Common Multiple Of 16 And 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.