What Is The Lowest Common Multiple Of 12 And 16
Juapaving
Apr 04, 2025 · 5 min read
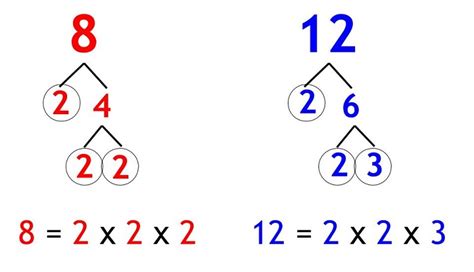
Table of Contents
What is the Lowest Common Multiple (LCM) of 12 and 16? A Deep Dive into Finding LCMs
Finding the lowest common multiple (LCM) might seem like a simple mathematical task, but understanding the underlying concepts and exploring different methods can significantly enhance your mathematical skills and problem-solving abilities. This comprehensive guide delves into the world of LCMs, focusing specifically on determining the LCM of 12 and 16, while also providing a broader understanding of the concept and its applications. We'll explore various methods, from prime factorization to the least common multiple formula and even using visual aids. Let's dive in!
Understanding Lowest Common Multiples (LCMs)
Before we tackle the specific problem of finding the LCM of 12 and 16, let's solidify our understanding of what an LCM actually is. The lowest common multiple, or LCM, of two or more integers is the smallest positive integer that is divisible by all of the integers. Think of it as the smallest number that contains all the numbers you're working with as factors.
For example, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
The common multiples of 2 and 3 are the numbers that appear in both lists: 6, 12, 18, 24... The lowest of these common multiples is 6. Therefore, the LCM of 2 and 3 is 6.
This concept extends to more than two numbers as well. Finding the LCM becomes increasingly important as we move into more complex mathematical areas like fractions, algebra, and even computer science.
Method 1: Prime Factorization to Find the LCM of 12 and 16
Prime factorization is a powerful technique for finding the LCM of any set of numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves. Let's apply this method to find the LCM of 12 and 16.
Step 1: Prime Factorization of 12
12 can be broken down as follows:
12 = 2 x 6 = 2 x 2 x 3 = 2² x 3
Step 2: Prime Factorization of 16
16 can be broken down as follows:
16 = 2 x 8 = 2 x 2 x 4 = 2 x 2 x 2 x 2 = 2⁴
Step 3: Identifying the Highest Powers of Each Prime Factor
Now, we identify the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2⁴ (from the factorization of 16).
- The highest power of 3 is 3¹ (from the factorization of 12).
Step 4: Calculating the LCM
To find the LCM, we multiply these highest powers together:
LCM(12, 16) = 2⁴ x 3¹ = 16 x 3 = 48
Therefore, the lowest common multiple of 12 and 16 is 48.
Method 2: Listing Multiples to Find the LCM of 12 and 16
This is a more straightforward, albeit potentially time-consuming, method, especially for larger numbers. We list the multiples of each number until we find the smallest common multiple.
Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120...
Multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160...
By comparing the two lists, we can see that the smallest number appearing in both lists is 48. Therefore, the LCM of 12 and 16 is 48.
Method 3: Using the Greatest Common Divisor (GCD) to Find the LCM
There's a relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula is:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- GCD(a, b) is the greatest common divisor of a and b.
- |a x b| represents the absolute value of a multiplied by b.
Let's apply this to our example:
Step 1: Find the GCD of 12 and 16
We can find the GCD using the Euclidean algorithm or prime factorization. Using prime factorization:
12 = 2² x 3 16 = 2⁴
The common prime factor is 2, and the lowest power is 2². Therefore, GCD(12, 16) = 4.
Step 2: Apply the LCM Formula
LCM(12, 16) = (12 x 16) / GCD(12, 16) = 192 / 4 = 48
Again, the LCM of 12 and 16 is 48.
Real-World Applications of LCM
Understanding LCMs isn't just about solving math problems; it has practical applications in various fields:
- Scheduling: Imagine two buses arrive at a stop at different intervals. Finding the LCM helps determine when both buses will arrive at the stop simultaneously.
- Construction: In construction projects, materials might need to be cut into specific lengths. Knowing the LCM ensures minimal waste.
- Music: LCMs are used in music theory to determine the least common multiple of different rhythmic patterns.
- Computer Science: LCMs are essential in algorithms related to scheduling and synchronization.
Conclusion: The LCM of 12 and 16 is 48
We've explored three different methods to calculate the lowest common multiple of 12 and 16, consistently arriving at the answer of 48. Understanding these methods empowers you to tackle more complex LCM problems and appreciate the broader applications of this fundamental mathematical concept. Remember that selecting the most efficient method depends on the context and the numbers involved. While listing multiples is simple for smaller numbers, prime factorization offers a more robust and efficient approach for larger numbers. The GCD method provides a powerful link between LCM and GCD, allowing for efficient calculation when the GCD is already known. Mastering these techniques will significantly enhance your mathematical proficiency and problem-solving skills. Now, go forth and conquer those LCMs!
Latest Posts
Latest Posts
-
Does A Parallelogram Have One Pair Of Parallel Sides
Apr 04, 2025
-
Algebraic Expressions Class 7 Practice Questions
Apr 04, 2025
-
What Is The Least Common Multiple Of 7 And 12
Apr 04, 2025
-
Base And Exponent Pdf With Answers 7th
Apr 04, 2025
-
How Many Inches Is One Meter
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lowest Common Multiple Of 12 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
