What Is The Least Common Multiple Of 9 And 24
Juapaving
May 13, 2025 · 5 min read
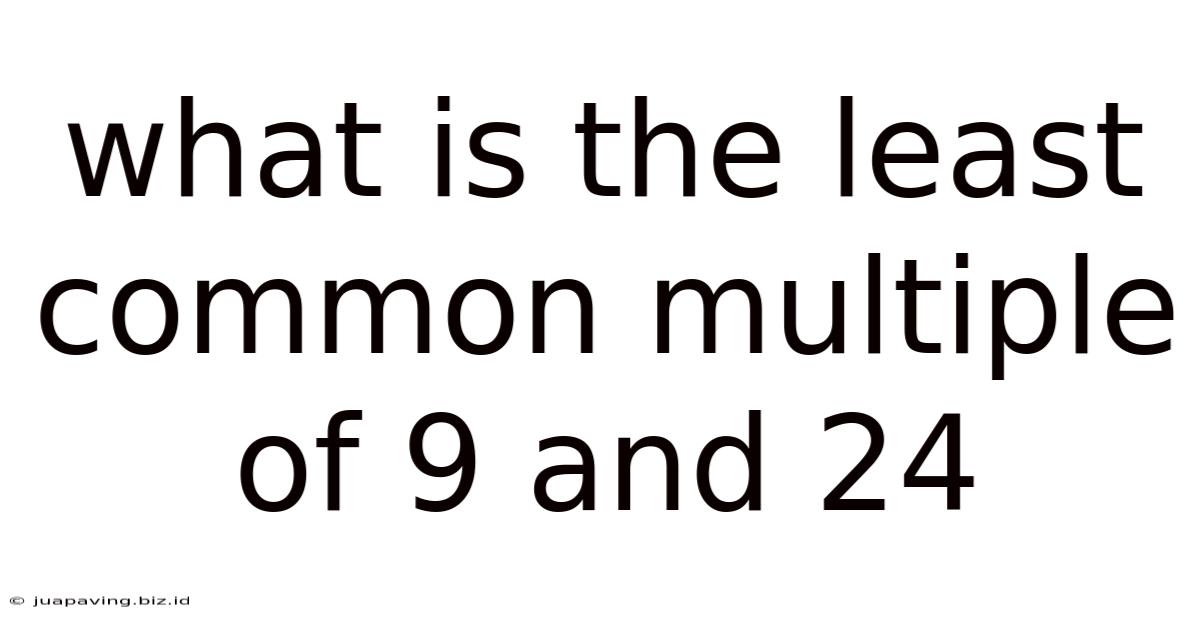
Table of Contents
What is the Least Common Multiple (LCM) of 9 and 24? A Deep Dive into Number Theory
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a deeper appreciation for number theory and its practical applications. This article will thoroughly explore how to find the LCM of 9 and 24, detailing various methods and explaining the mathematical principles involved. We'll delve into prime factorization, the greatest common divisor (GCD), and the relationship between LCM and GCD, providing you with a comprehensive understanding of this fundamental concept.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3. Finding the LCM is crucial in various mathematical problems, including simplifying fractions, solving equations, and working with rhythmic patterns in music.
Method 1: Prime Factorization
This method is arguably the most fundamental and widely used for finding the LCM. It leverages the concept of prime factorization, which breaks down a number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Find the Prime Factorization of Each Number
- 9: The prime factorization of 9 is 3 x 3 or 3².
- 24: The prime factorization of 24 is 2 x 2 x 2 x 3 or 2³ x 3.
Step 2: Identify the Highest Power of Each Prime Factor
Compare the prime factorizations of 9 and 24. We have the prime factors 2 and 3.
- 2: The highest power of 2 is 2³ (from the factorization of 24).
- 3: The highest power of 3 is 3² (from the factorization of 9).
Step 3: Multiply the Highest Powers Together
Multiply the highest powers of each prime factor identified in Step 2:
2³ x 3² = 8 x 9 = 72
Therefore, the least common multiple of 9 and 24 is 72.
Method 2: Listing Multiples
This method is straightforward but can become less efficient for larger numbers. It involves listing the multiples of each number until you find the smallest common multiple.
Step 1: List Multiples of 9
Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90…
Step 2: List Multiples of 24
Multiples of 24: 24, 48, 72, 96, 120…
Step 3: Identify the Smallest Common Multiple
By comparing the lists, we see that the smallest common multiple of 9 and 24 is 72.
Method 3: Using the GCD (Greatest Common Divisor)
The LCM and GCD are intimately related. Knowing the GCD allows us to calculate the LCM efficiently, particularly for larger numbers.
Step 1: Find the GCD of 9 and 24
We can use the Euclidean algorithm to find the GCD.
- Divide 24 by 9: 24 = 2 x 9 + 6
- Divide 9 by the remainder 6: 9 = 1 x 6 + 3
- Divide 6 by the remainder 3: 6 = 2 x 3 + 0
The last non-zero remainder is 3, so the GCD of 9 and 24 is 3.
Step 2: Apply the LCM-GCD Relationship Formula
The formula connecting LCM and GCD is:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers. Substituting the values:
LCM(9, 24) x 3 = 9 x 24
LCM(9, 24) = (9 x 24) / 3 = 216 / 3 = 72
This confirms that the LCM of 9 and 24 is 72.
Applications of LCM
Understanding LCM has significant practical applications across various fields:
1. Fraction Simplification: Finding the Least Common Denominator (LCD)
When adding or subtracting fractions, the LCM of the denominators is crucial. It helps find the least common denominator (LCD), enabling efficient addition and subtraction. For example, adding 1/9 and 1/24 requires finding the LCD, which is the LCM of 9 and 24 (72).
2. Cyclic Events: Determining When Events Coincide
Imagine two events that occur cyclically. For instance, one event happens every 9 days, and another every 24 days. The LCM (72) tells us when both events will coincide again—after 72 days. This is applicable in various scenarios, from scheduling tasks to predicting celestial phenomena.
3. Rhythmic Patterns in Music: Finding the Common Beat
In music, LCM helps determine the common beat or the point where different rhythmic patterns align. Understanding LCM allows musicians to create complex and harmonious musical compositions.
Conclusion: Mastering the LCM
Finding the least common multiple of 9 and 24, as demonstrated through prime factorization, listing multiples, and utilizing the GCD, highlights the importance of understanding fundamental number theory concepts. The LCM isn't just a simple calculation; it's a key building block in various mathematical applications, extending to real-world problems in scheduling, music, and beyond. Mastering the LCM empowers you with a deeper understanding of number relationships and their practical implications. This knowledge is invaluable for anyone pursuing mathematical studies or working with numerical data. The methods outlined provide flexible tools adaptable to various mathematical contexts and scenarios, making the calculation of LCM accessible and efficient regardless of the numbers involved. Remember to choose the method that best suits your needs and the complexity of the problem at hand.
Latest Posts
Latest Posts
-
Where Would Go On A Number Line
May 13, 2025
-
Whats The Prime Factorization Of 76
May 13, 2025
-
Which Of The Following Is Not A Type Of Carbohydrate
May 13, 2025
-
Greatest Common Factor Of 36 And 90
May 13, 2025
-
Which Is An Example Of A Heterogeneous Mixture
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 9 And 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.