What Is The Least Common Multiple Of 18 And 30
Juapaving
May 10, 2025 · 5 min read
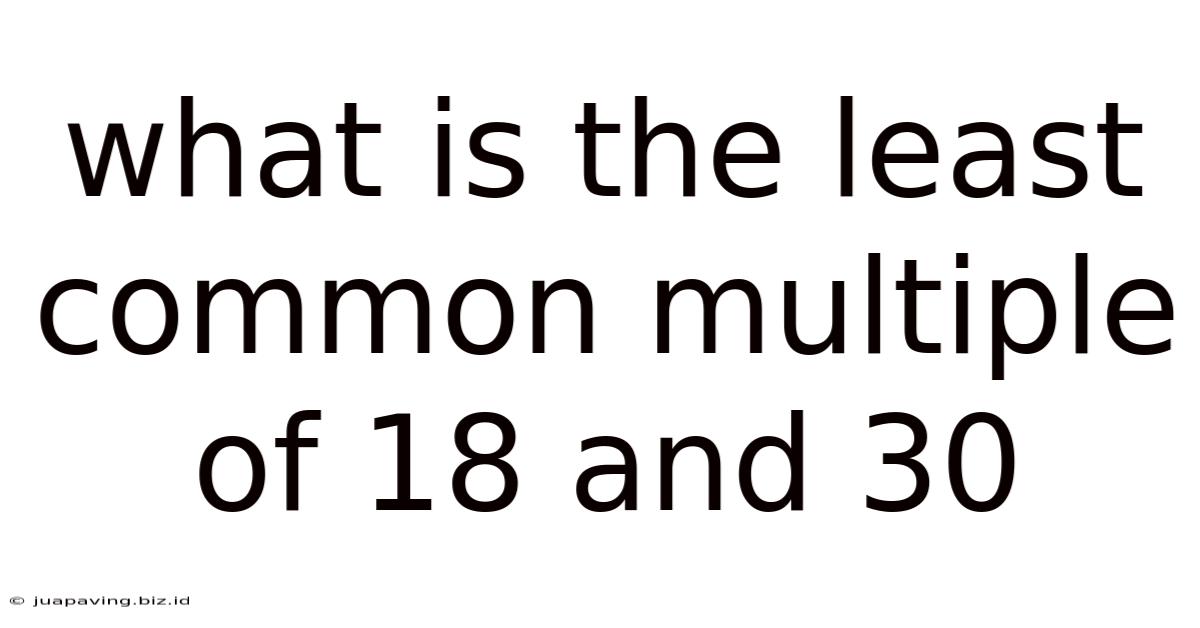
Table of Contents
What is the Least Common Multiple (LCM) of 18 and 30? A Deep Dive into Finding the LCM
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it is crucial for various mathematical applications. This comprehensive guide delves into the intricacies of finding the LCM of 18 and 30, exploring multiple approaches, and providing a solid foundation for tackling similar problems. We'll go beyond simply stating the answer, focusing on the why and how to ensure you fully grasp the process.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers without leaving a remainder. Think of it as the smallest number that contains all the prime factors of the given numbers. This concept is fundamental in various areas, including:
- Fraction operations: Finding the LCM is essential when adding or subtracting fractions with different denominators. The LCM of the denominators becomes the common denominator.
- Scheduling problems: LCM helps determine the time when events with different repeating cycles will coincide. For instance, finding when two machines with different operational cycles will simultaneously complete a task.
- Modular arithmetic: LCM plays a key role in solving congruence problems and other advanced mathematical concepts.
Methods for Finding the LCM of 18 and 30
There are several effective methods to determine the LCM, each with its own advantages and disadvantages. We'll explore three common approaches:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
Multiples of 18: 18, 36, 54, 72, 90, 108, 126, 144, 162, 180...
Multiples of 30: 30, 60, 90, 120, 150, 180, 210...
By comparing the lists, we observe that the smallest common multiple is 90. This method works well for smaller numbers but becomes inefficient for larger numbers.
2. Prime Factorization Method
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
Prime Factorization of 18: 18 = 2 x 3 x 3 = 2¹ x 3²
Prime Factorization of 30: 30 = 2 x 3 x 5 = 2¹ x 3¹ x 5¹
To find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2¹
- The highest power of 3 is 3²
- The highest power of 5 is 5¹
Therefore, the LCM(18, 30) = 2¹ x 3² x 5¹ = 2 x 9 x 5 = 90
3. Greatest Common Divisor (GCD) Method
This method uses the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula is:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, we need to find the GCD of 18 and 30. We can use the Euclidean algorithm for this:
- Divide the larger number (30) by the smaller number (18): 30 ÷ 18 = 1 with a remainder of 12.
- Replace the larger number with the smaller number (18) and the smaller number with the remainder (12): 18 ÷ 12 = 1 with a remainder of 6.
- Repeat the process: 12 ÷ 6 = 2 with a remainder of 0.
- The last non-zero remainder is the GCD, which is 6.
Now, we can use the formula:
LCM(18, 30) = (18 x 30) / 6 = 540 / 6 = 90
Comparing the Methods
Each method provides the same result, but their efficiency varies. The listing method is simple for small numbers but becomes impractical for larger ones. Prime factorization is generally efficient and easily scales to larger numbers. The GCD method is also efficient, particularly when the GCD is easily found.
Applications of LCM in Real-World Scenarios
Beyond the realm of pure mathematics, LCM finds practical applications in various real-world scenarios:
- Construction and Engineering: Determining the optimal spacing or alignment of materials in construction projects, ensuring consistent patterns and minimizing waste.
- Manufacturing and Production: Synchronizing machinery cycles in manufacturing processes to maximize efficiency and output.
- Scheduling and Time Management: Coordinating events with varying cycles, like bus schedules or factory shifts.
- Music Theory: Determining the least common multiple of note durations in musical compositions.
- Computer Science: Solving synchronization problems in concurrent programming.
- Cryptography: Utilizing the properties of LCM in certain cryptographic algorithms.
Advanced Concepts Related to LCM
While finding the LCM of two numbers is relatively straightforward, understanding the broader context involves exploring related concepts such as:
- LCM of more than two numbers: The process extends to multiple numbers; you repeatedly apply the LCM calculation to pairs of numbers until you arrive at the LCM of all the numbers.
- Least Common Multiple and Greatest Common Divisor (GCD): The LCM and GCD are intrinsically linked. Their product is always equal to the product of the two original numbers (a x b = LCM(a,b) x GCD(a,b)). This relationship is often used in efficient LCM calculation algorithms.
- Euclidean Algorithm: This algorithm is an efficient method for finding the GCD of two numbers, which is then used in the GCD method for finding the LCM. Understanding this algorithm is crucial for advanced mathematical computations.
- Modular Arithmetic and Congruences: The LCM plays a vital role in solving congruence problems, which have implications in cryptography and other fields.
Conclusion: Mastering the LCM
This detailed exploration of finding the least common multiple of 18 and 30 showcases the importance of understanding different approaches. While the answer, 90, is relatively straightforward, the underlying concepts and multiple methods used to arrive at the answer are fundamental for tackling more complex mathematical problems and real-world applications. Mastering the LCM concept enhances your mathematical toolkit and opens doors to a broader understanding of number theory and its applications across various disciplines. Remember to select the most appropriate method based on the complexity of the numbers involved, prioritizing efficiency and accuracy. The ability to confidently calculate the LCM contributes significantly to your problem-solving skills and enhances your overall mathematical proficiency.
Latest Posts
Latest Posts
-
Volume Of 1 Mole Gas At Stp
May 11, 2025
-
A Car Is Travelling On A Straight Road
May 11, 2025
-
What Is The Fraction Of 40 Percent
May 11, 2025
-
Action Verbs That Begin With E
May 11, 2025
-
Copper Cannot Displace Zinc From Its Salt Solution
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 18 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.