What Is The Least Common Multiple Of 18 And 21
Juapaving
May 09, 2025 · 5 min read
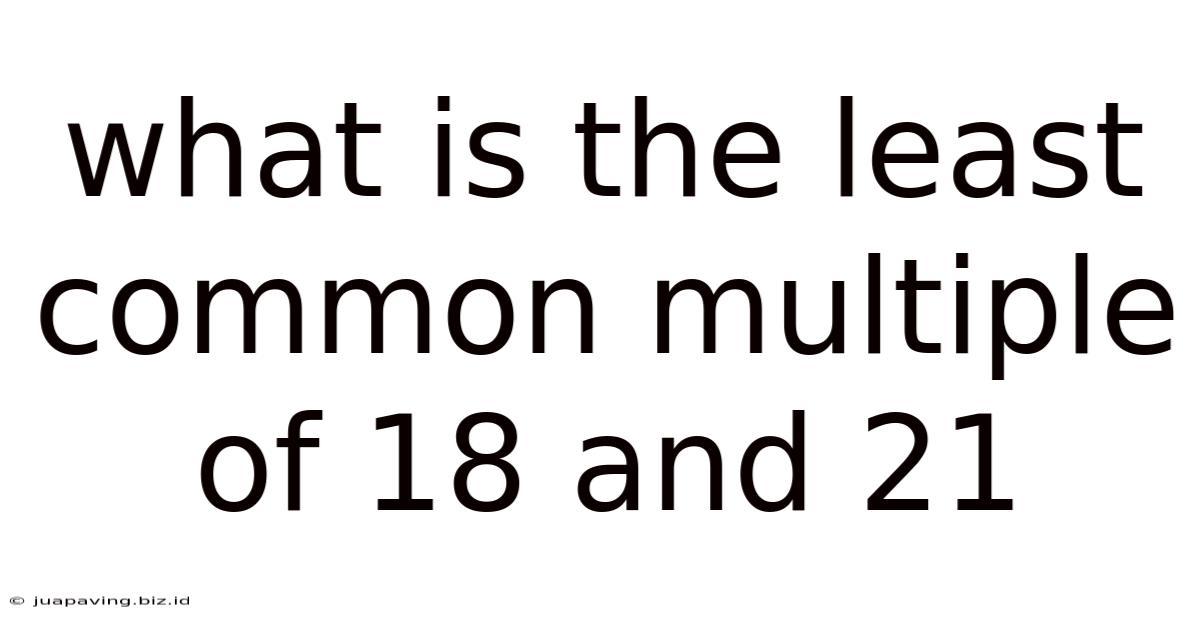
Table of Contents
What is the Least Common Multiple (LCM) of 18 and 21? A Deep Dive into Finding LCMs
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it provides a valuable foundation in number theory and is crucial for various applications in mathematics, computer science, and even music theory. This article will explore the LCM of 18 and 21 in detail, examining various approaches, explaining the underlying principles, and providing a deeper understanding of this fundamental concept.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers in question as factors. For instance, the LCM of 2 and 3 is 6, as 6 is the smallest number that is divisible by both 2 and 3. This concept extends to more than two integers as well.
Understanding LCM is critical in various fields:
- Fractions: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Scheduling: Determining when events that occur at regular intervals will coincide (e.g., buses arriving at a stop) utilizes LCM.
- Music Theory: Rhythmic patterns and musical intervals often rely on LCM calculations.
- Computer Science: Algorithms for solving certain problems (like finding the least common multiple of a set of integers) are used in various applications.
Methods for Finding the LCM of 18 and 21
Several methods exist to calculate the LCM of two numbers, including 18 and 21. Let's explore the most common ones:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
Multiples of 18: 18, 36, 54, 72, 90, 108, 126, ...
Multiples of 21: 21, 42, 63, 84, 105, 126, ...
Notice that 126 is the smallest multiple present in both lists. Therefore, the LCM of 18 and 21 is 126.
This method becomes less efficient with larger numbers, making other methods preferable.
2. Prime Factorization Method
This is a more efficient and systematic method for finding the LCM, especially for larger numbers. It involves finding the prime factorization of each number.
Prime Factorization of 18: 2 x 3 x 3 = 2 x 3²
Prime Factorization of 21: 3 x 7
To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(18, 21) = 2 x 3² x 7 = 2 x 9 x 7 = 126
This method is generally preferred due to its efficiency and systematic approach. It works well for any number of integers.
3. Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are related through the following formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, we need to find the GCD of 18 and 21. We can use the Euclidean algorithm for this:
- Divide the larger number (21) by the smaller number (18): 21 = 18 x 1 + 3
- Replace the larger number with the smaller number (18) and the smaller number with the remainder (3): 18 = 3 x 6 + 0
- The GCD is the last non-zero remainder, which is 3.
Now, we can use the formula:
LCM(18, 21) = (18 x 21) / 3 = 378 / 3 = 126
This method is also efficient and demonstrates the relationship between LCM and GCD.
Why Understanding LCM is Important
The seemingly simple task of finding the LCM has far-reaching implications across various disciplines. Let's explore some real-world applications:
-
Project Scheduling: Imagine you have two tasks that need to be completed. Task A takes 18 days and Task B takes 21 days. If you want to know when both tasks will be completed simultaneously, assuming they start at the same time, you need to find the LCM(18, 21). The answer, 126 days, indicates the next time both tasks will be finished together.
-
Synchronization in Computer Systems: In computer programming, multiple processes might need to synchronize their actions. Determining the least common multiple of different process cycles can help optimize synchronization, preventing conflicts and improving efficiency.
-
Music and Rhythm: Musicians frequently use LCM to understand rhythmic patterns and create harmonies. For example, the LCM of two note durations determines when the rhythms will align, creating a sense of musical resolution.
-
Inventory Management: Imagine a business stocking two products with different reorder cycles. One product needs reordering every 18 days, and the other every 21 days. Finding the LCM can optimize inventory management and ensure efficient stock replenishment.
Beyond the Basics: Extending LCM Concepts
The concept of LCM extends beyond just two numbers. You can find the LCM of three or more numbers using the same prime factorization method. Simply find the prime factorization of each number, take the highest power of each prime factor, and multiply them together.
Conclusion: Mastering LCM Calculations
Finding the least common multiple of 18 and 21, as demonstrated, is achievable through various methods. The prime factorization method is generally preferred for its efficiency and applicability to larger numbers and multiple integers. Understanding LCM is not just about solving mathematical problems; it's about grasping a fundamental concept with significant applications in various fields, emphasizing the importance of number theory in our daily lives and across diverse disciplines. By mastering LCM calculations, you gain a powerful tool for tackling problems ranging from simple fraction addition to complex scheduling challenges. The ability to efficiently calculate LCM showcases a fundamental understanding of mathematical relationships and opens doors to deeper exploration in number theory and related fields.
Latest Posts
Latest Posts
-
Do Liquids Have A Fixed Shape
May 10, 2025
-
320 Km Is How Many Miles
May 10, 2025
-
Energy Stored In The Nucleus Of An Atom Is Called
May 10, 2025
-
What Is 2 Out Of 3 As A Percentage
May 10, 2025
-
What Percentage Is 100 Of 250
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 18 And 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.