What Is The Least Common Multiple Of 16 And 40
Juapaving
May 10, 2025 · 5 min read
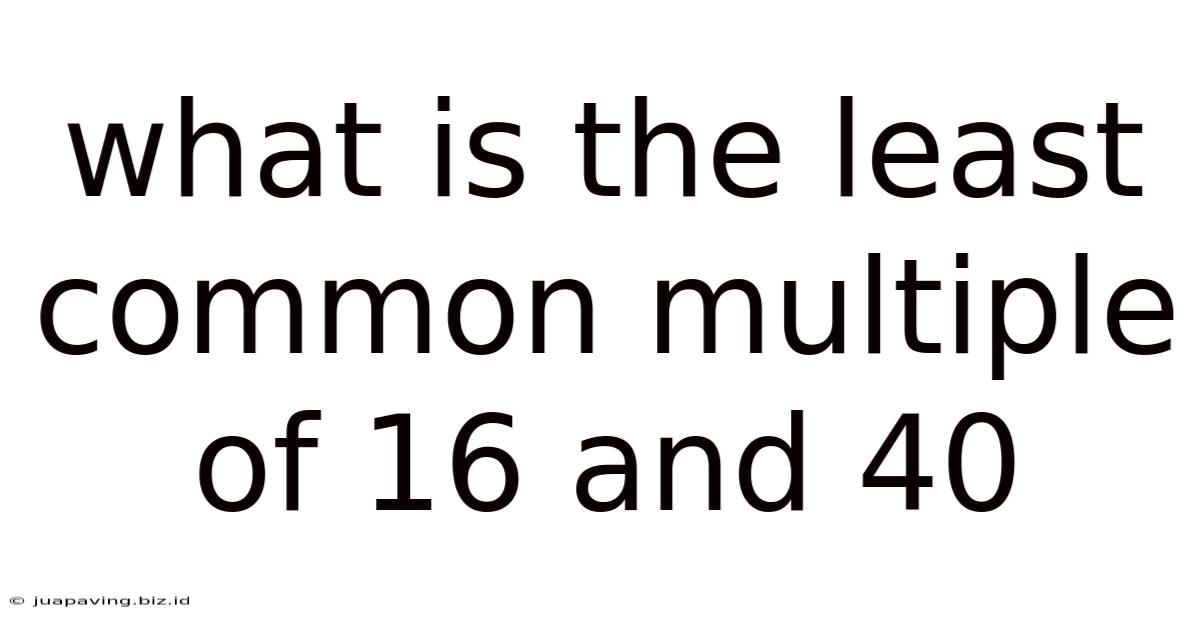
Table of Contents
What is the Least Common Multiple (LCM) of 16 and 40? A Deep Dive into Finding the LCM
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex problems in number theory and beyond. This article will delve deep into determining the LCM of 16 and 40, exploring multiple methods and providing a comprehensive understanding of the underlying principles. We'll go beyond simply finding the answer and unpack the 'why' behind each calculation, making this a valuable resource for students and anyone seeking a clearer grasp of LCM.
Understanding Least Common Multiple (LCM)
Before jumping into the calculation, let's solidify our understanding of LCM. The least common multiple of two or more integers is the smallest positive integer that is a multiple of each of the numbers. In simpler terms, it's the smallest number that both (or all) of the given numbers can divide into evenly.
Think of it like finding the smallest common ground between different sets of multiples. For instance, the multiples of 2 are 2, 4, 6, 8, 10, 12... and the multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both sequences is 6, making 6 the LCM of 2 and 3.
Method 1: Listing Multiples
The most straightforward method for finding the LCM, especially for smaller numbers like 16 and 40, is to list the multiples of each number until a common multiple is found.
Multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160...
Multiples of 40: 40, 80, 120, 160, 200...
Notice that 80 appears in both lists. However, a smaller common multiple, 80, appears first. Therefore, the LCM of 16 and 40 is 80. This method is simple for smaller numbers but becomes less practical as the numbers get larger.
Advantages of the Listing Method:
- Intuitive and easy to understand: This method is perfect for beginners grasping the concept of LCM.
- Requires minimal mathematical knowledge: No advanced formulas or prime factorization is needed.
Disadvantages of the Listing Method:
- Time-consuming for larger numbers: Listing multiples for large numbers can be incredibly tedious and prone to errors.
- Not practical for finding the LCM of multiple numbers: This method becomes significantly more complex when dealing with three or more numbers.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, is using prime factorization. This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime factorization of 16: 2 x 2 x 2 x 2 = 2⁴
Prime factorization of 40: 2 x 2 x 2 x 5 = 2³ x 5
To find the LCM using prime factorization:
- Identify the prime factors: We have 2 and 5.
- Find the highest power of each prime factor: The highest power of 2 is 2⁴ (from the factorization of 16), and the highest power of 5 is 5¹ (from the factorization of 40).
- Multiply the highest powers together: 2⁴ x 5¹ = 16 x 5 = 80
Therefore, the LCM of 16 and 40 is 80.
Advantages of the Prime Factorization Method:
- Efficient for larger numbers: This method is significantly faster than listing multiples for larger numbers.
- Works well for multiple numbers: The prime factorization method can easily be extended to find the LCM of three or more numbers.
Disadvantages of the Prime Factorization Method:
- Requires understanding of prime numbers and factorization: This method assumes a basic understanding of prime numbers and the ability to factorize numbers effectively.
- Can be challenging for very large numbers: While more efficient, factorizing extremely large numbers can still be computationally intensive.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The GCD is the largest number that divides both numbers evenly. We can use the following formula to find the LCM:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- |a x b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
Let's apply this to 16 and 40:
-
Find the GCD of 16 and 40: The factors of 16 are 1, 2, 4, 8, 16. The factors of 40 are 1, 2, 4, 5, 8, 10, 20, 40. The greatest common factor is 8.
-
Apply the formula: LCM(16, 40) = (16 x 40) / 8 = 640 / 8 = 80
Therefore, the LCM of 16 and 40 is 80.
Advantages of the GCD Method:
- Efficient and less prone to error: This method provides a systematic way to calculate the LCM, especially when dealing with larger numbers.
- Utilizes the relationship between LCM and GCD: This method highlights the important connection between these two fundamental mathematical concepts.
Disadvantages of the GCD Method:
- Requires finding the GCD first: An extra step is involved in determining the GCD before calculating the LCM.
- May require knowledge of different GCD finding methods: Depending on the complexity of the numbers, finding the GCD might involve using the Euclidean algorithm or other methods.
Real-World Applications of LCM
Understanding LCM is more than just an academic exercise. It has numerous practical applications in various fields:
- Scheduling: Determining when events will coincide (e.g., when two buses arrive at the same stop simultaneously).
- Fraction operations: Finding a common denominator when adding or subtracting fractions.
- Music theory: Calculating the least common multiple of note durations in musical compositions.
- Engineering: In projects requiring synchronized components or processes.
- Construction: Coordinating work schedules involving different teams or processes.
Conclusion: The LCM of 16 and 40 is 80
Through three different methods—listing multiples, prime factorization, and the GCD method—we've conclusively demonstrated that the least common multiple of 16 and 40 is 80. Choosing the most appropriate method depends on the specific context and the numbers involved. For smaller numbers, listing multiples might suffice, while for larger numbers, prime factorization or the GCD method offers a more efficient approach. Understanding the concept of LCM and mastering different calculation methods empowers you to tackle more complex mathematical problems and opens doors to various practical applications. Remember, grasping the underlying principles is as important as knowing the final answer. The more you understand the 'why', the more confident and proficient you'll become in your mathematical abilities.
Latest Posts
Latest Posts
-
Screwdriver Is What Type Of Simple Machine
May 10, 2025
-
What Is The Largest Organelle In The Cell
May 10, 2025
-
Difference Between Molecular Mass And Molar Mass
May 10, 2025
-
How To Find Lateral Surface Area Of A Cone
May 10, 2025
-
Essay On Laughter Is Best Medicine
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 16 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.