What Is The Least Common Factor Of 9 And 15
Juapaving
Apr 03, 2025 · 5 min read
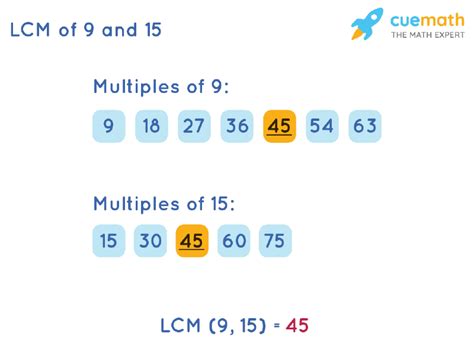
Table of Contents
- What Is The Least Common Factor Of 9 And 15
- Table of Contents
- What is the Least Common Factor of 9 and 15? A Deep Dive into Number Theory
- Understanding the Terminology: GCD vs. LCM
- Methods for Finding the GCD of 9 and 15
- 1. Listing Factors
- 2. Prime Factorization
- 3. Euclidean Algorithm
- The Significance of the GCD
- 1. Fraction Simplification
- 2. Cryptography
- 3. Computer Science
- 4. Modular Arithmetic
- 5. Abstract Algebra
- Beyond the Numbers: Understanding the Concept
- Further Exploration: Exploring LCM and their Relationship
- Conclusion: The GCD – A Foundation of Number Theory
- Latest Posts
- Latest Posts
- Related Post
What is the Least Common Factor of 9 and 15? A Deep Dive into Number Theory
Finding the least common factor (LCF) might seem like a simple arithmetic task, but understanding the underlying principles unlocks a deeper appreciation for number theory and its applications in various fields. While the term "least common factor" isn't standard mathematical terminology (it's usually referred to as the greatest common divisor or GCD, or sometimes the highest common factor or HCF), we'll explore the concept thoroughly, clarifying the confusion and then focusing on finding the GCD of 9 and 15 using several methods. We'll then examine the broader significance of this seemingly simple concept.
Understanding the Terminology: GCD vs. LCM
Before we dive into finding the greatest common divisor (GCD) of 9 and 15, let's clarify the terminology. The terms "least common factor" and "greatest common divisor" are sometimes used interchangeably, leading to confusion. It's crucial to understand the difference.
-
Greatest Common Divisor (GCD): This is the largest number that divides both numbers without leaving a remainder. It's also known as the highest common factor (HCF). This is the term we'll primarily use in this article.
-
Least Common Multiple (LCM): This is the smallest positive number that is a multiple of both numbers.
In our case, we're looking for the GCD of 9 and 15. Finding the LCM is a related, but distinct, problem.
Methods for Finding the GCD of 9 and 15
Several methods can effectively determine the GCD of two numbers. Let's explore the most common approaches:
1. Listing Factors
The simplest method is to list all the factors of each number and identify the largest common factor.
Factors of 9: 1, 3, 9 Factors of 15: 1, 3, 5, 15
The common factors are 1 and 3. Therefore, the GCD(9, 15) = 3.
2. Prime Factorization
This method involves expressing each number as a product of its prime factors. The GCD is then the product of the common prime factors raised to the lowest power.
Prime factorization of 9: 3 x 3 = 3² Prime factorization of 15: 3 x 5
The only common prime factor is 3, and its lowest power is 3¹. Therefore, the GCD(9, 15) = 3.
3. Euclidean Algorithm
This is a highly efficient method for finding the GCD of two numbers, especially for larger numbers. It's based on the principle that the GCD of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCD.
Let's apply the Euclidean algorithm to 9 and 15:
- 15 = 9 x 1 + 6 (Subtract 9 from 15, the remainder is 6)
- 9 = 6 x 1 + 3 (Subtract 6 from 9, the remainder is 3)
- 6 = 3 x 2 + 0 (Subtract 3 from 6, the remainder is 0)
The last non-zero remainder is 3, so the GCD(9, 15) = 3.
The Significance of the GCD
The GCD, while seemingly a simple concept, has far-reaching applications in various mathematical and computational fields. Here are some key areas:
1. Fraction Simplification
The GCD is fundamental to simplifying fractions. To simplify a fraction, we divide both the numerator and the denominator by their GCD. For example, the fraction 15/9 can be simplified to 5/3 by dividing both the numerator and denominator by their GCD, which is 3.
2. Cryptography
The GCD plays a crucial role in various cryptographic algorithms, such as the RSA algorithm, which is widely used for secure communication over the internet. The algorithm relies heavily on the properties of prime numbers and their greatest common divisors.
3. Computer Science
The Euclidean algorithm for finding the GCD is a cornerstone of computer science, particularly in areas like computer graphics and algorithm design. Its efficiency and simplicity make it a valuable tool for solving various computational problems.
4. Modular Arithmetic
GCD is essential in modular arithmetic, which deals with remainders after division. It's used to determine whether a linear congruence has a solution.
5. Abstract Algebra
The concept of GCD extends to more abstract algebraic structures, such as rings and ideals, where it plays a crucial role in understanding the structure of these mathematical objects.
Beyond the Numbers: Understanding the Concept
The calculation of the GCD of 9 and 15 is just a starting point. The real value lies in understanding the broader implications and applications of this fundamental mathematical concept. It highlights the interconnectedness of various mathematical fields and its importance in solving real-world problems.
Further Exploration: Exploring LCM and their Relationship
While we focused on the GCD, it's worth briefly exploring the relationship between the GCD and the Least Common Multiple (LCM). For any two positive integers a and b, the product of their GCD and LCM is equal to the product of the two numbers. In other words:
GCD(a, b) x LCM(a, b) = a x b
For 9 and 15:
GCD(9, 15) = 3 LCM(9, 15) = 45
Therefore: 3 x 45 = 135, and 9 x 15 = 135. This relationship further underscores the interconnected nature of these fundamental concepts.
Conclusion: The GCD – A Foundation of Number Theory
The seemingly simple task of finding the greatest common divisor of 9 and 15 opens a window into the fascinating world of number theory. Understanding the various methods for calculating the GCD, coupled with an appreciation for its broader applications, provides a strong foundation for further exploration of mathematical concepts and their impact on diverse fields. From simplifying fractions to securing online transactions, the GCD proves that even seemingly basic arithmetic operations can have profound consequences. The next time you encounter a problem involving the GCD, remember the elegance and power of this fundamental concept.
Latest Posts
Latest Posts
-
How Many Spades Are In A Deck Of 52
Apr 08, 2025
-
The Most Abundant Gas In Air Is
Apr 08, 2025
-
Moment Of Inertia Of A Square Plate
Apr 08, 2025
-
Common Multiples Of 7 And 9
Apr 08, 2025
-
How Many Terms In A Polynomial
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Factor Of 9 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.