What Is The Least Common Denominator Of 12 And 16
Juapaving
Apr 04, 2025 · 5 min read
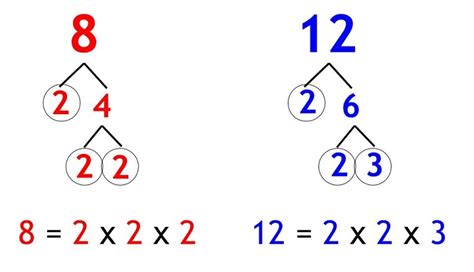
Table of Contents
What is the Least Common Denominator (LCD) of 12 and 16? A Deep Dive into Finding the LCD
Finding the least common denominator (LCD) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it provides a strong foundation in mathematics, particularly crucial for more advanced topics like algebra and calculus. This comprehensive guide will not only answer the question – what is the least common denominator of 12 and 16? – but also delve into the 'why' and 'how' behind finding the LCD, exploring various techniques and their applications.
Understanding Least Common Denominator (LCD)
The least common denominator (LCD), also known as the least common multiple (LCM) of the denominators, is the smallest number that is a multiple of all the denominators involved. It's a fundamental concept in adding, subtracting, and comparing fractions. When fractions have different denominators, we need to find a common denominator before we can perform these operations. The LCD simplifies the process, ensuring we use the smallest possible number, making calculations easier and results cleaner.
Why is the LCD important?
-
Adding and Subtracting Fractions: You can't directly add or subtract fractions with different denominators. Finding the LCD allows you to rewrite the fractions with a common denominator, enabling the addition or subtraction of the numerators.
-
Comparing Fractions: Determining which fraction is larger or smaller is straightforward when they share a common denominator. The LCD makes this comparison efficient.
-
Simplifying Expressions: In algebra and other advanced mathematical contexts, finding the LCD is crucial for simplifying complex expressions involving fractions.
Methods for Finding the LCD of 12 and 16
Let's find the LCD of 12 and 16 using several different methods. This will solidify your understanding and show you various approaches suitable for different scenarios.
Method 1: Listing Multiples
This method is straightforward and easy to visualize, particularly for smaller numbers.
-
List the multiples of each number:
- Multiples of 12: 12, 24, 36, 48, 60, 72, 96, ...
- Multiples of 16: 16, 32, 48, 64, 80, 96, ...
-
Identify the common multiples: Observe that 48 and 96 are common multiples of both 12 and 16.
-
Determine the least common multiple: The smallest common multiple is 48. Therefore, the LCD of 12 and 16 is 48.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a systematic approach.
-
Find the prime factorization of each number:
- 12 = 2 x 2 x 3 = 2² x 3
- 16 = 2 x 2 x 2 x 2 = 2⁴
-
Identify the highest power of each prime factor: The prime factors involved are 2 and 3. The highest power of 2 is 2⁴ (from 16), and the highest power of 3 is 3¹ (from 12).
-
Multiply the highest powers together: 2⁴ x 3 = 16 x 3 = 48
Therefore, the LCD of 12 and 16 is 48. This method is generally preferred for its efficiency and applicability to larger numbers.
Method 3: Greatest Common Divisor (GCD) Method
This method uses the relationship between the LCM (Least Common Multiple) and GCD (Greatest Common Divisor). The formula connecting them is:
LCM(a, b) = (a x b) / GCD(a, b)
-
Find the GCD of 12 and 16: The GCD is the largest number that divides both 12 and 16 without leaving a remainder. Using the Euclidean algorithm or prime factorization, we find the GCD(12, 16) = 4.
-
Apply the formula: LCM(12, 16) = (12 x 16) / 4 = 192 / 4 = 48
Therefore, the LCD of 12 and 16 is 48. This method showcases the elegant connection between LCM and GCD.
Applications of Finding the LCD
The ability to find the LCD extends far beyond simple fraction arithmetic. It's a fundamental skill with wide-ranging applications in:
-
Algebra: Solving equations involving fractions often requires finding the LCD to simplify the equation and solve for the unknown variable.
-
Calculus: In integral calculus, finding the LCD is sometimes necessary when dealing with rational functions (functions expressed as ratios of polynomials).
-
Real-world problems: Many real-world problems involve fractions and ratios, such as dividing resources, calculating proportions, and determining quantities. The LCD becomes essential for solving these problems accurately.
Example: Adding Fractions with LCD
Let's demonstrate the practical application of finding the LCD in adding fractions. Consider the following problem:
1/12 + 1/16 = ?
-
Find the LCD: As we've already established, the LCD of 12 and 16 is 48.
-
Rewrite the fractions with the common denominator:
- 1/12 = (1 x 4) / (12 x 4) = 4/48
- 1/16 = (1 x 3) / (16 x 3) = 3/48
-
Add the fractions:
- 4/48 + 3/48 = (4 + 3) / 48 = 7/48
Therefore, 1/12 + 1/16 = 7/48. Without finding the LCD, this addition would be impossible.
Beyond the Basics: Finding LCD for More Than Two Numbers
The methods described above can be extended to find the LCD of more than two numbers. The prime factorization method is particularly well-suited for this, as you simply consider all the prime factors involved and their highest powers.
Conclusion: Mastering the LCD
Finding the least common denominator is a crucial skill in mathematics, with applications extending far beyond basic fraction arithmetic. Understanding the various methods – listing multiples, prime factorization, and the GCD method – allows you to choose the most efficient approach depending on the complexity of the numbers involved. Mastering the LCD is essential for success in algebra, calculus, and many real-world problem-solving scenarios. The ability to confidently calculate the LCD not only simplifies calculations but also deepens your understanding of fundamental mathematical concepts. Remember that the key lies not just in getting the right answer (which is 48 for 12 and 16), but also in understanding the underlying principles and choosing the appropriate method for efficiency and accuracy.
Latest Posts
Latest Posts
-
Cross Sectional Area Of A Cylinder Formula
Apr 04, 2025
-
Current Cannot Flow Through A Circuit When The Switch Is
Apr 04, 2025
-
How Many Square Feet Is 20 X 20 Feet
Apr 04, 2025
-
Relation Between Electric Field And Potential
Apr 04, 2025
-
800 Sq M To Sq Ft
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Denominator Of 12 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
