What Is The Lcm Of 8 12
Juapaving
Apr 04, 2025 · 5 min read
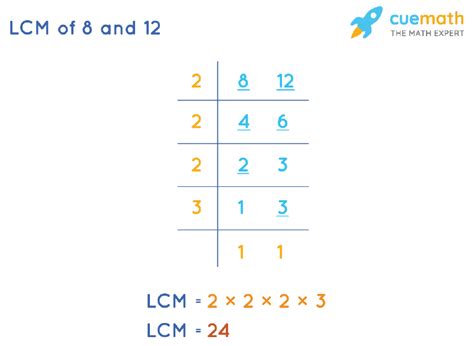
Table of Contents
What is the LCM of 8 and 12? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics with wide-ranging applications, from simplifying fractions to solving complex problems in algebra and beyond. This comprehensive guide will not only answer the question, "What is the LCM of 8 and 12?" but will also delve into the various methods for calculating LCMs, exploring their practical applications and providing you with a robust understanding of the concept.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 8 and 12, let's solidify our understanding of the concept itself. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The common multiples of 2 and 3 are 6, 12, 18, and so on. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Methods for Calculating the LCM
Several methods can be employed to calculate the least common multiple. Let's explore the most common and efficient approaches:
1. Listing Multiples Method
This is the most straightforward method, particularly suitable for smaller numbers. You list the multiples of each number until you find the smallest multiple common to both.
- Multiples of 8: 8, 16, 24, 32, 40, 48...
- Multiples of 12: 12, 24, 36, 48, 60...
The smallest common multiple is 24. Therefore, the LCM of 8 and 12 is 24.
This method becomes less practical as the numbers get larger.
2. Prime Factorization Method
This method leverages the prime factorization of each number. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
To find the LCM using prime factorization:
- Identify all the prime factors present in the numbers. In this case, we have 2 and 3.
- For each prime factor, take the highest power present in the factorizations. The highest power of 2 is 2³ (from 8), and the highest power of 3 is 3¹ (from 12).
- Multiply these highest powers together: 2³ x 3¹ = 8 x 3 = 24.
Therefore, the LCM of 8 and 12 is 24. This method is significantly more efficient for larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) of two numbers are related through the following formula:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
First, we need to find the GCD of 8 and 12. We can use the Euclidean algorithm for this:
- Divide the larger number (12) by the smaller number (8): 12 ÷ 8 = 1 with a remainder of 4.
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (4): 8 ÷ 4 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 4.
Now, we can use the formula:
LCM(8, 12) x GCD(8, 12) = 8 x 12 LCM(8, 12) x 4 = 96 LCM(8, 12) = 96 ÷ 4 = 24
Therefore, the LCM of 8 and 12 is 24. This method is also efficient, particularly when dealing with larger numbers where finding the GCD is easier than directly finding the LCM.
Applications of LCM
The concept of LCM finds applications in diverse fields:
-
Fraction Addition and Subtraction: Finding the LCM of the denominators is crucial when adding or subtracting fractions with different denominators. This ensures that we are working with equivalent fractions with a common denominator.
-
Scheduling Problems: LCM helps in solving scheduling problems where events repeat at different intervals. For instance, if two buses arrive at a stop every 8 and 12 minutes respectively, the LCM (24 minutes) indicates when they will arrive simultaneously.
-
Modular Arithmetic: LCM plays a key role in modular arithmetic, which deals with remainders after division.
-
Music Theory: LCM is used in music theory to determine the least common multiple of the note durations in a musical piece to find a common time signature.
-
Engineering and Design: LCM is used in various engineering applications, for instance in calculating the optimal gear ratios in machinery.
Solving Similar Problems
Let's extend our understanding by tackling a few more examples:
Example 1: Find the LCM of 15 and 20.
Using the prime factorization method:
- 15 = 3 x 5
- 20 = 2² x 5
LCM(15, 20) = 2² x 3 x 5 = 60
Example 2: Find the LCM of 18, 24, and 36.
Using the prime factorization method:
- 18 = 2 x 3²
- 24 = 2³ x 3
- 36 = 2² x 3²
LCM(18, 24, 36) = 2³ x 3² = 72
Example 3: Find the LCM of 10, 15 and 35
Using Prime Factorization
*10 = 2 x 5 *15 = 3 x 5 *35 = 5 x 7
LCM(10, 15, 35) = 2 x 3 x 5 x 7 = 210
Conclusion
In conclusion, the least common multiple (LCM) of 8 and 12 is 24. We've explored multiple methods for calculating the LCM, highlighting their strengths and weaknesses. Understanding the LCM is essential for a wide array of mathematical applications, extending beyond basic arithmetic into more advanced areas. Mastering these methods empowers you to tackle more complex problems with confidence and efficiency, strengthening your mathematical foundation. Remember to choose the method best suited to the numbers you're working with, prioritizing efficiency and accuracy.
Latest Posts
Latest Posts
-
A Negatively Charged Particle In An Atom Is The
Apr 04, 2025
-
Common Passageway Of Food And Air
Apr 04, 2025
-
Which Equation Represents A Fission Reaction
Apr 04, 2025
-
34 Important Laws Of Physics Pdf
Apr 04, 2025
-
How Many Grams Are In 4 Kg
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 8 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
