What Is The Lcm Of 8 10
Juapaving
Apr 06, 2025 · 5 min read
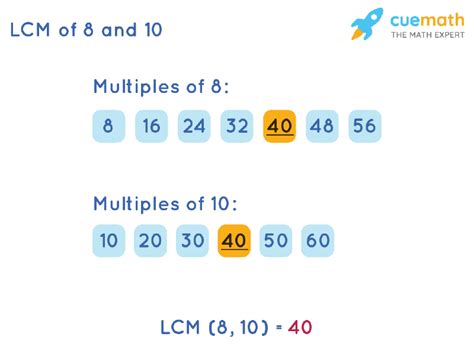
Table of Contents
Unveiling the LCM: A Deep Dive into Finding the Least Common Multiple of 8 and 10
Finding the Least Common Multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and exploring different methods can unlock a deeper appreciation for number theory and its applications. This comprehensive guide will not only reveal the LCM of 8 and 10 but also equip you with the knowledge to tackle similar problems and understand the broader context of LCMs in mathematics and beyond.
What is a Least Common Multiple (LCM)?
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers. Think of it as the smallest number that contains all the given numbers as factors. This concept has widespread applications in various fields, from scheduling tasks to simplifying fractions and solving problems in algebra and geometry.
Methods for Finding the LCM
Several methods exist for calculating the LCM, each offering a unique approach to the problem. Let's explore the most common and effective strategies:
1. Listing Multiples Method
This method, while straightforward, can become tedious for larger numbers. It involves listing the multiples of each number until a common multiple is found. The smallest common multiple is then the LCM.
Let's illustrate this with 8 and 10:
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...
The smallest common multiple in both lists is 40. Therefore, the LCM of 8 and 10 is 40.
This method is suitable for smaller numbers but becomes impractical for larger ones.
2. Prime Factorization Method
This method is significantly more efficient, especially when dealing with larger numbers. It leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
Steps:
-
Find the prime factorization of each number:
- 8 = 2 x 2 x 2 = 2³
- 10 = 2 x 5
-
Identify the highest power of each prime factor:
- The prime factors are 2 and 5.
- The highest power of 2 is 2³ = 8
- The highest power of 5 is 5¹ = 5
-
Multiply the highest powers together:
- LCM(8, 10) = 2³ x 5 = 8 x 5 = 40
Therefore, the LCM of 8 and 10 is 40. This method is generally preferred for its efficiency and applicability to larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) of two numbers are closely related. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers.
Formula: LCM(a, b) x GCD(a, b) = a x b
To use this method:
-
Find the GCD of 8 and 10:
- The factors of 8 are 1, 2, 4, 8.
- The factors of 10 are 1, 2, 5, 10.
- The greatest common factor is 2. Therefore, GCD(8, 10) = 2.
-
Apply the formula:
- LCM(8, 10) x 2 = 8 x 10
- LCM(8, 10) = (8 x 10) / 2 = 40
Thus, the LCM of 8 and 10 is 40. This method is efficient if you already know the GCD. Finding the GCD can be done using the Euclidean algorithm, which is particularly useful for larger numbers.
Understanding the Significance of LCM
The LCM isn't just a mathematical curiosity; it has practical applications in various real-world scenarios:
-
Scheduling: Imagine two buses arrive at a stop every 8 and 10 minutes, respectively. The LCM (40 minutes) represents the time when both buses will arrive simultaneously at the stop again.
-
Fraction Arithmetic: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator, simplifying the calculation.
-
Cyclic Patterns: In scenarios involving repeating patterns or cycles, the LCM helps determine when those patterns will coincide. This is useful in various fields like engineering and computer science.
-
Music Theory: The LCM is used in music theory to find the least common multiple of the lengths of different musical phrases, aiding in the creation of harmonious musical structures.
Beyond Two Numbers: Finding the LCM of Multiple Numbers
The methods described above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly well-suited for this. For example, to find the LCM of 8, 10, and 12:
-
Prime Factorization:
- 8 = 2³
- 10 = 2 x 5
- 12 = 2² x 3
-
Highest Powers:
- Highest power of 2 is 2³ = 8
- Highest power of 3 is 3¹ = 3
- Highest power of 5 is 5¹ = 5
-
Multiplication:
- LCM(8, 10, 12) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
Therefore, the LCM of 8, 10, and 12 is 120.
The Importance of Understanding Number Theory
The concept of LCM is deeply rooted in number theory, a branch of mathematics that explores the properties of integers. Mastering concepts like LCM and GCD provides a strong foundation for further mathematical exploration, particularly in areas like abstract algebra and cryptography.
Practical Applications and Real-World Examples
Beyond the examples already mentioned, the LCM finds its place in diverse applications:
-
Construction and Engineering: Calculating the optimal lengths for materials or aligning structures often involves finding the LCM.
-
Manufacturing and Production: Coordinating different production cycles or scheduling machinery maintenance can benefit from LCM calculations.
-
Computer Science: Algorithms and data structures often rely on LCM calculations for efficient resource management.
Conclusion: Mastering the LCM for Mathematical Proficiency
The LCM, while seemingly a simple concept, holds significant mathematical weight and practical utility. Understanding the different methods for calculating the LCM, particularly the prime factorization method, empowers you to tackle more complex problems efficiently. Furthermore, appreciating the deeper connections between LCM, GCD, and number theory enhances your mathematical understanding and problem-solving abilities. The LCM of 8 and 10, as we've demonstrated, is 40. However, the true value lies in grasping the underlying principles and their diverse applications in the world around us. By mastering this fundamental concept, you'll not only solve mathematical problems but also gain a sharper understanding of numerical relationships and their practical significance.
Latest Posts
Latest Posts
-
The Energy In Motion Is Called
Apr 09, 2025
-
How Many Black Spades Are In A Deck Of Cards
Apr 09, 2025
-
What Percent Of 28 Is 21
Apr 09, 2025
-
Common Multiples Of 5 And 15
Apr 09, 2025
-
How To Find Center Of Mass Of A Triangle
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 8 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.