What Is The Lcm Of 6 12 And 15
Juapaving
Apr 08, 2025 · 5 min read
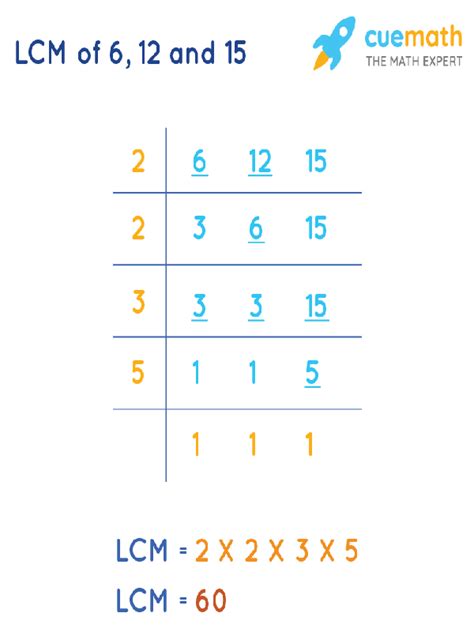
Table of Contents
What is the LCM of 6, 12, and 15? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications ranging from simplifying fractions to solving complex problems in algebra and beyond. This article will not only answer the question "What is the LCM of 6, 12, and 15?" but also delve deep into the underlying principles, providing you with a comprehensive understanding of LCM calculations and their practical significance. We'll explore different methods for finding the LCM, emphasizing efficiency and clarity.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors. For instance, the LCM of 2 and 3 is 6, because 6 is the smallest number divisible by both 2 and 3.
Why is the LCM important? The LCM is a vital tool in various mathematical operations, including:
- Adding and subtracting fractions: Finding a common denominator is essential when adding or subtracting fractions. The LCM of the denominators serves as the least common denominator (LCD).
- Solving problems involving cycles and periods: Problems involving repetitive events, like the meeting of trains or the synchronization of machines, often utilize the LCM to find the time until the events align.
- Simplifying algebraic expressions: LCM plays a role in simplifying rational expressions and reducing fractions to their lowest terms.
- Number theory: LCM is a fundamental concept in number theory, used in various advanced calculations and proofs.
Methods for Calculating the LCM
Several methods exist for finding the least common multiple of numbers. We'll explore the most common and efficient approaches:
1. Listing Multiples Method
This is the most straightforward method, suitable for small numbers. You list the multiples of each number until you find the smallest multiple common to all.
Let's find the LCM of 6, 12, and 15 using this method:
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
- Multiples of 12: 12, 24, 36, 48, 60, ...
- Multiples of 15: 15, 30, 45, 60, ...
The smallest multiple common to all three lists is 60. Therefore, the LCM(6, 12, 15) = 60.
Limitations: This method becomes cumbersome and inefficient when dealing with larger numbers or a greater number of integers.
2. Prime Factorization Method
This method is more efficient and works well for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
Steps:
-
Find the prime factorization of each number:
- 6 = 2 x 3
- 12 = 2 x 2 x 3 = 2² x 3
- 15 = 3 x 5
-
Identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
-
Multiply the highest powers together: LCM = 2² x 3 x 5 = 4 x 3 x 5 = 60
Therefore, the LCM(6, 12, 15) = 60.
Advantages: This method is systematic and works efficiently for larger numbers and more integers. It provides a deeper understanding of the number's structure.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of a set of numbers are related. Using the GCD, we can calculate the LCM efficiently.
The relationship between LCM and GCD is given by the formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
This formula can be extended to more than two numbers. However, calculating the GCD for multiple numbers requires iterative application. Let's illustrate this with our example:
-
Find the GCD of 6 and 12: Using the Euclidean algorithm (a common method for finding the GCD), we find that GCD(6, 12) = 6.
-
Find the GCD of the result (6) and 15: GCD(6, 15) = 3.
-
Apply the LCM formula (this needs slight adaptation for multiple numbers): We can't directly apply the two-number formula. Instead, we use the prime factorization method which implicitly uses the GCD concept, as seen previously. This method is preferable for multiple numbers as the generalized two-number formula becomes complex.
The Answer: LCM(6, 12, 15) = 60
Using all three methods, we consistently find that the least common multiple of 6, 12, and 15 is 60. This means 60 is the smallest positive integer that is divisible by 6, 12, and 15 without leaving a remainder.
Practical Applications of LCM
The concept of LCM extends far beyond simple mathematical exercises. It has significant practical implications in various fields:
-
Scheduling and Time Management: Imagine three buses depart from a station at different intervals: one every 6 minutes, another every 12 minutes, and a third every 15 minutes. The LCM (60 minutes) tells us when all three buses will depart simultaneously again.
-
Manufacturing and Production: Machines operating in a factory might have different cycle times. The LCM of these cycle times determines the frequency at which all machines complete their cycles simultaneously, allowing for efficient synchronization.
-
Music and Rhythm: In music, the LCM is used to determine the least common denominator for musical rhythms and time signatures, enabling the creation of harmonious and synchronized musical compositions.
Conclusion: Mastering LCM Calculations
Understanding and calculating the least common multiple is a valuable skill with numerous applications. While the listing multiples method offers a simple approach for smaller numbers, the prime factorization method provides a more efficient and robust solution for larger numbers and a greater number of integers. Mastering these methods equips you to tackle various mathematical problems and real-world situations involving cyclical events and common denominators. The LCM of 6, 12, and 15, as we've comprehensively demonstrated, is 60. This seemingly simple calculation underscores the power and importance of this fundamental mathematical concept. Remember to choose the method best suited to the problem at hand – focusing on efficiency and understanding. With practice, you'll become proficient in solving LCM problems with confidence and ease.
Latest Posts
Latest Posts
-
Log 1 2 3 Log1 Log2 Log3
Apr 08, 2025
-
How Many Valence Electrons Does Alkali Metals Have
Apr 08, 2025
-
100 Words To Describe Your Mom
Apr 08, 2025
-
What Is A Multiple Of 17
Apr 08, 2025
-
Lines That Belong To The Same Plane And Never Intersect
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 6 12 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.