What Is The Lcm Of 54 And 36
Juapaving
May 11, 2025 · 4 min read
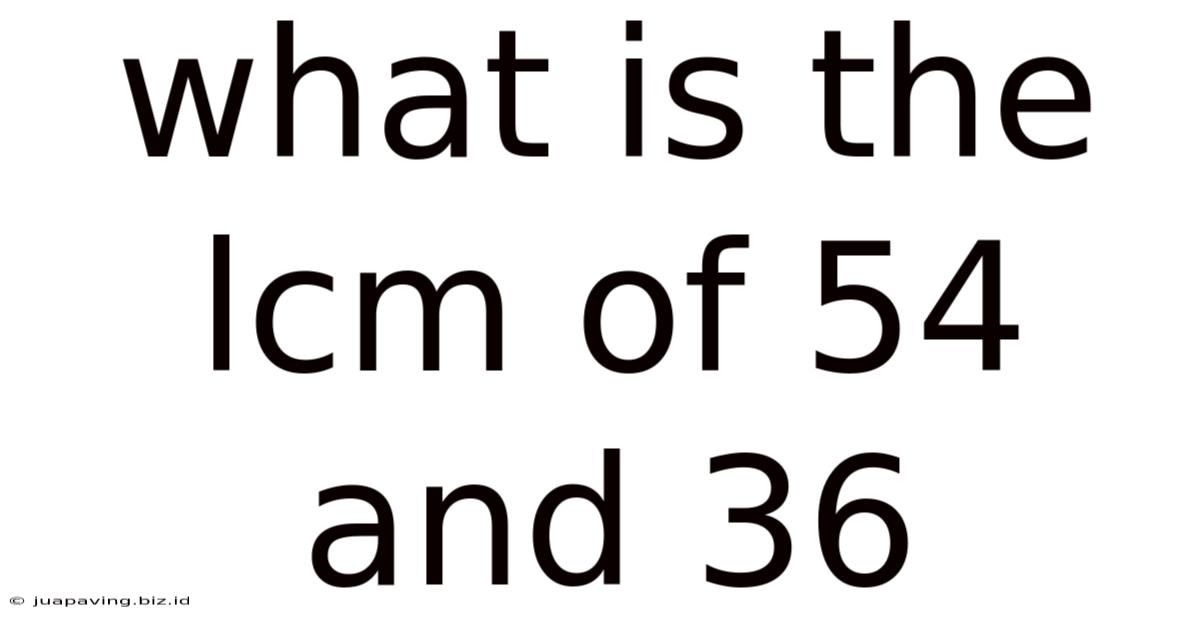
Table of Contents
What is the LCM of 54 and 36? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics with wide-ranging applications in various fields, from simplifying fractions to solving complex problems in physics and engineering. This comprehensive guide will explore the LCM of 54 and 36, providing multiple methods to calculate it, explaining the underlying concepts, and showcasing its practical significance.
Understanding Least Common Multiples (LCM)
Before delving into the specific calculation for 54 and 36, let's establish a solid understanding of what LCM represents. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers. It's essentially the smallest number that contains all the numbers as factors.
For example, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... and the multiples of 3 are 3, 6, 9, 12, 15... The common multiples of 2 and 3 are 6, 12, 18, and so on. The smallest of these common multiples is 6, hence the LCM(2,3) = 6.
Methods to Calculate LCM(54, 36)
We will now explore various methods to determine the LCM of 54 and 36. Each method offers a unique approach and strengthens our understanding of the concept.
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of both 54 and 36 until we find the smallest common multiple.
Multiples of 54: 54, 108, 162, 216, 270, 324, 378, 432, 486, 540...
Multiples of 36: 36, 72, 108, 144, 180, 216, 252, 288, 324, 360, 432...
By comparing the lists, we observe that the smallest common multiple is 108. Therefore, LCM(54, 36) = 108. However, this method becomes less efficient with larger numbers.
Method 2: Prime Factorization
This is a more efficient and systematic method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
Prime factorization of 54: 2 x 3 x 3 x 3 = 2¹ x 3³
Prime factorization of 36: 2 x 2 x 3 x 3 = 2² x 3²
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2² = 4
- Highest power of 3: 3³ = 27
Now, multiply these highest powers together: 4 x 27 = 108. Therefore, LCM(54, 36) = 108.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are related by the following formula:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 54 and 36 using the Euclidean algorithm:
- 54 = 36 x 1 + 18
- 36 = 18 x 2 + 0
The GCD is 18.
Now, we can use the formula:
LCM(54, 36) = (54 x 36) / GCD(54, 36) = (54 x 36) / 18 = 108
This method is particularly useful when dealing with larger numbers where prime factorization might be more time-consuming.
Applications of LCM
The concept of LCM finds extensive applications in diverse areas:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
-
Scheduling Problems: Determining when events with different periodicities will coincide, such as the meeting of two buses or trains with different schedules.
-
Gear Ratios and Rotational Mechanics: In mechanical engineering, LCM is crucial for calculating gear ratios and analyzing rotational speeds of interconnected gears.
-
Cyclic Processes: In physics and chemistry, LCM is useful in understanding and predicting the timing of recurring events in cyclical processes.
-
Music Theory: Determining the least common multiple of note durations is important in music composition and theory.
Why Understanding LCM is Crucial
Mastering the concept of LCM is essential for:
-
Problem-solving skills: It enhances your ability to approach and solve mathematical problems systematically and efficiently.
-
Mathematical foundation: It forms a crucial building block for more advanced mathematical concepts.
-
Real-world applications: It provides a practical tool for solving problems in various fields, as highlighted above.
Conclusion: The Power of 108
We have successfully demonstrated through multiple methods that the least common multiple of 54 and 36 is 108. This seemingly simple calculation exemplifies a fundamental mathematical concept with vast practical implications across numerous disciplines. Understanding the different methods for finding the LCM empowers you to tackle complex problems with confidence and efficiency, solidifying your mathematical foundation and expanding your problem-solving capabilities. Remember to choose the method most suitable for the numbers involved; prime factorization is generally preferred for larger numbers, while the GCD method can be efficient when the GCD is easily calculated. The ability to swiftly and accurately find the LCM of numbers is a valuable skill applicable in various facets of life.
Latest Posts
Latest Posts
-
What Is The Lcm Of 40 And 32
May 11, 2025
-
Which Statement About Gases Is True
May 11, 2025
-
How To Minus Percentage From Price
May 11, 2025
-
Which Of These Is An Example Of Kinetic Energy
May 11, 2025
-
Differentiate Between Monohybrid Cross And Dihybrid Cross
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 54 And 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.