What Is The Lcm Of 4 8 And 10
Juapaving
May 11, 2025 · 5 min read
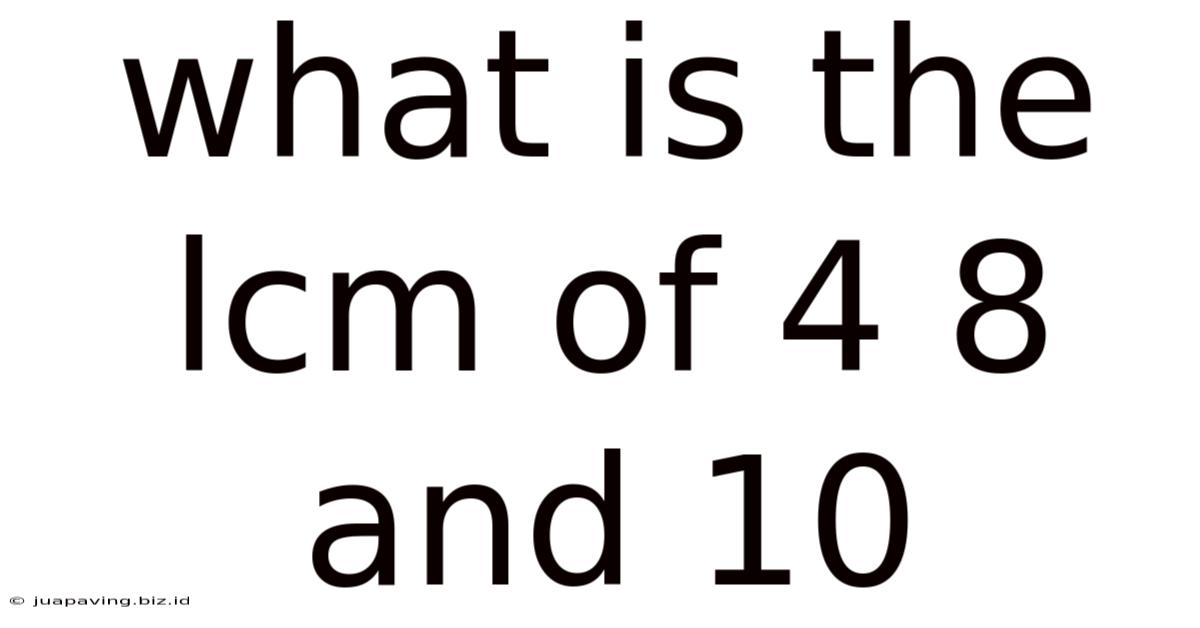
Table of Contents
What is the LCM of 4, 8, and 10? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, with applications spanning various fields from simple arithmetic to complex programming and engineering. This article will thoroughly explore how to calculate the LCM of 4, 8, and 10, providing multiple methods to understand the process and its underlying principles. We'll also delve into the broader concept of LCMs and their significance.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the given numbers as factors. This concept is crucial in various mathematical operations, including simplifying fractions, solving problems involving ratios and proportions, and scheduling events that occur at regular intervals.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers, is to list the multiples of each number until you find the smallest common multiple.
Steps:
- List multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48...
- List multiples of 8: 8, 16, 24, 32, 40, 48, 56...
- List multiples of 10: 10, 20, 30, 40, 50, 60...
By comparing the lists, we can see that the smallest number appearing in all three lists is 40. Therefore, the LCM of 4, 8, and 10 is 40.
This method works well for smaller numbers, but becomes increasingly inefficient as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a more systematic approach. It relies on expressing each number as a product of its prime factors. Prime factorization involves breaking down a number into its prime components (numbers only divisible by 1 and themselves).
Steps:
-
Find the prime factorization of each number:
- 4 = 2 x 2 = 2²
- 8 = 2 x 2 x 2 = 2³
- 10 = 2 x 5
-
Identify the highest power of each prime factor present:
- The prime factors are 2 and 5.
- The highest power of 2 is 2³ (from the factorization of 8).
- The highest power of 5 is 5¹ (from the factorization of 10).
-
Multiply the highest powers together: 2³ x 5¹ = 8 x 5 = 40
Therefore, the LCM of 4, 8, and 10 is 40 using the prime factorization method. This method is generally preferred for its efficiency and systematic nature, especially when dealing with larger numbers or a greater number of integers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of a set of numbers are closely related. There's a formula that connects them:
LCM(a, b) * GCD(a, b) = a * b
This formula works for two numbers. For more than two numbers, we need to apply it iteratively. Let's demonstrate this with our example.
Steps:
-
Find the GCD of 4 and 8: The GCD of 4 and 8 is 4 (since 4 is the largest number that divides both 4 and 8).
-
Use the formula for two numbers: LCM(4, 8) * GCD(4, 8) = 4 * 8 LCM(4, 8) * 4 = 32 LCM(4, 8) = 32 / 4 = 8
-
Now find the LCM of 8 and 10 using the same principle: First, find the GCD of 8 and 10. The GCD of 8 and 10 is 2. LCM(8, 10) * GCD(8, 10) = 8 * 10 LCM(8, 10) * 2 = 80 LCM(8, 10) = 80 / 2 = 40
Therefore, the LCM of 4, 8, and 10 is 40.
Method 4: Using a Calculator or Software
Many calculators and mathematical software packages have built-in functions to calculate the LCM of numbers directly. Inputting the numbers 4, 8, and 10 into such a tool will instantly provide the result: 40. This is a convenient method for quick calculations, especially when dealing with larger or more complex sets of numbers.
Applications of LCM
The LCM has practical applications in various fields:
-
Scheduling: Determining when events that repeat at different intervals will occur simultaneously. For example, if one event happens every 4 days, another every 8 days, and a third every 10 days, the LCM (40) indicates they will all occur together again after 40 days.
-
Fraction Arithmetic: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is simply the LCM of the denominators.
-
Gears and Pulleys: In mechanical engineering, the LCM helps calculate the synchronization of gears or pulleys with different numbers of teeth or revolutions per minute.
-
Digital Signal Processing: LCM calculations are involved in the synchronization and sampling rates of digital signals.
-
Music Theory: LCMs are sometimes used in musical composition to determine the least common multiple of note durations.
-
Project Management: Calculating the time it takes for multiple independent tasks to align.
Conclusion
Calculating the LCM of 4, 8, and 10, as demonstrated through various methods, highlights the importance of understanding fundamental mathematical concepts. While listing multiples provides a simple approach for smaller numbers, prime factorization offers a more efficient and systematic solution for larger numbers. Using the relationship between LCM and GCD provides another alternative, and calculators or software offer a quick solution. Understanding the LCM and its applications opens doors to solving more complex mathematical problems and extends its relevance to various real-world scenarios. The consistent result across all methods—40—reinforces the validity and reliability of each approach. The selection of the best method often depends on the complexity of the numbers involved and the available tools. Regardless of the method chosen, understanding the underlying principles of LCM is key to mastering this crucial mathematical concept.
Latest Posts
Latest Posts
-
Finding The Distance Between Two Parallel Lines
May 11, 2025
-
Which Of The Following Are Characteristics Of Viruses
May 11, 2025
-
How Far Is 50 Km By Car
May 11, 2025
-
Which Organelle Is The Control Center Of A Cell
May 11, 2025
-
Compare And Contrast Alcoholic Fermentation And Lactic Acid Fermentation
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 4 8 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.