What Is The Lcm Of 4 6 12
Juapaving
May 12, 2025 · 4 min read
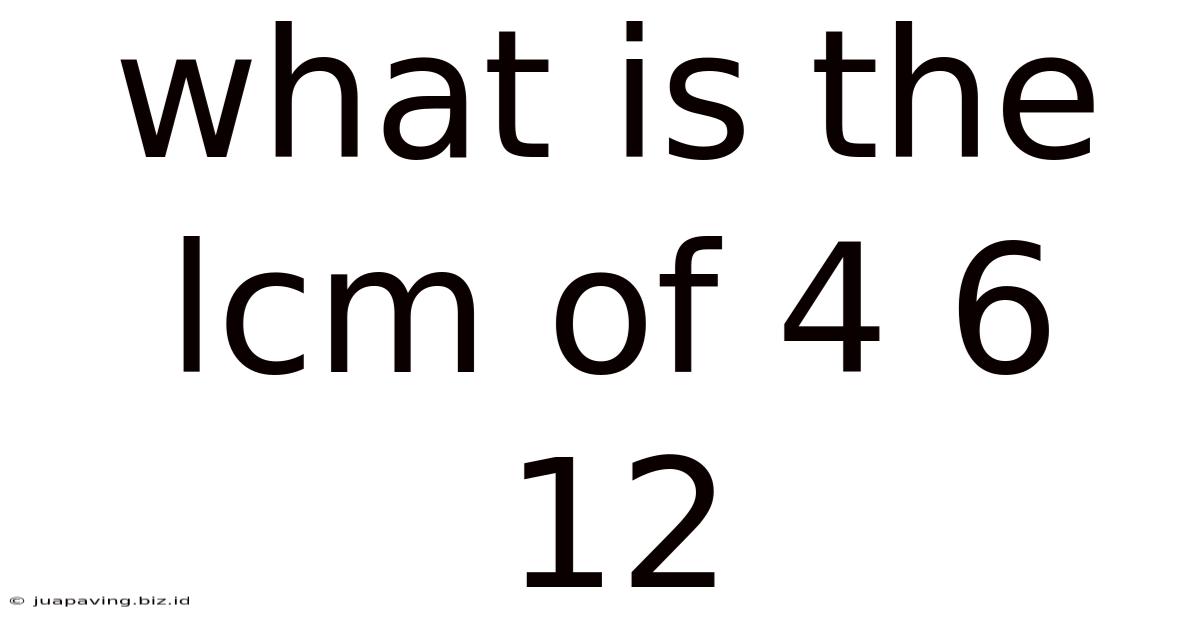
Table of Contents
What is the LCM of 4, 6, and 12? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it is crucial for a strong foundation in mathematics. This article will delve into the question: What is the LCM of 4, 6, and 12? We'll explore not just the answer, but also the different approaches to solving this problem, the importance of LCM in various fields, and some practical applications.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 4, 6, and 12, let's establish a firm understanding of what an LCM actually is.
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be evenly divided by all the given numbers without leaving a remainder.
For example, the multiples of 4 are 4, 8, 12, 16, 20... The multiples of 6 are 6, 12, 18, 24, 30... The multiples of 12 are 12, 24, 36, 48...
Notice that 12 appears in all three lists. Is it the smallest number that appears in all three lists? Yes. Therefore, the LCM of 4, 6, and 12 is 12.
Methods for Calculating LCM
There are several methods to calculate the LCM of a set of numbers. Let's examine the most common ones:
1. Listing Multiples Method
This method, as demonstrated above, involves listing the multiples of each number until a common multiple is found. It's simple for small numbers but becomes cumbersome and inefficient for larger numbers.
- Advantages: Easy to understand and visualize, especially for beginners.
- Disadvantages: Inefficient for larger numbers, prone to errors with manual calculation.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. It's a more efficient and systematic approach, particularly for larger numbers.
Steps:
-
Find the prime factorization of each number:
- 4 = 2 x 2 = 2²
- 6 = 2 x 3
- 12 = 2 x 2 x 3 = 2² x 3
-
Identify the highest power of each prime factor:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
-
Multiply the highest powers together:
- LCM(4, 6, 12) = 2² x 3 = 4 x 3 = 12
- Advantages: Efficient and systematic, especially for larger numbers. Less prone to errors.
- Disadvantages: Requires knowledge of prime factorization.
3. Greatest Common Divisor (GCD) Method
This method uses the relationship between the LCM and the greatest common divisor (GCD) of the numbers. The formula is:
LCM(a, b, c...) = (|a x b x c...|) / GCD(a, b, c...)
Where |a x b x c...| represents the absolute value of the product of all numbers.
To find the GCD, you can use the Euclidean algorithm or prime factorization. Let's use prime factorization for our example:
-
Find the prime factorization of each number (as done in method 2):
- 4 = 2²
- 6 = 2 x 3
- 12 = 2² x 3
-
Find the GCD: The common prime factors are 2 (with the lowest power of 2¹) and 3. Therefore, GCD(4, 6, 12) = 2¹ x 1 = 2
-
Apply the formula: LCM(4, 6, 12) = (4 x 6 x 12) / 2 = 288 / 2 = 12
- Advantages: Relatively efficient, utilizes the GCD which is also a useful concept.
- Disadvantages: Requires calculating both LCM and GCD, may be slightly more complex for beginners.
Importance of LCM in Various Fields
The concept of LCM extends far beyond simple arithmetic exercises. It finds applications in various fields, including:
1. Scheduling and Planning
LCM is crucial in scheduling tasks that need to be performed at regular intervals. For example, if three machines need servicing every 4, 6, and 12 days respectively, the LCM (12) determines when all three machines will need servicing simultaneously.
2. Fractions and Rational Numbers
LCM plays a vital role in adding and subtracting fractions with different denominators. Finding the LCM of the denominators allows for the conversion of fractions to a common denominator, simplifying the calculations.
3. Music Theory
In music theory, LCM is used to determine the least common multiple of different note durations, helping to calculate the length of musical phrases and identify points of rhythmic convergence.
4. Engineering and Physics
The concept of LCM can be found in various engineering and physics applications, particularly in situations involving periodic phenomena like oscillations and wave patterns.
Conclusion
Determining the LCM of 4, 6, and 12, as we've seen, yields an answer of 12. However, the significance of this calculation extends beyond a simple numerical result. Understanding the different methods for finding the LCM – listing multiples, prime factorization, and the GCD method – empowers you to approach similar problems with efficiency and accuracy. Furthermore, recognizing the broader applications of LCM across various disciplines underscores its importance as a fundamental mathematical concept. Mastering this concept will undoubtedly enhance your problem-solving skills and deepen your understanding of mathematical principles. The seemingly simple question, "What is the LCM of 4, 6, and 12?" thus opens doors to a wealth of mathematical insight and real-world applications.
Latest Posts
Latest Posts
-
What Are The Three Main Categories Of Elements
May 12, 2025
-
Disadvantages Of Parliamentary Form Of Government
May 12, 2025
-
The Cell The Basic Unit Of Life
May 12, 2025
-
Whats The Difference Between A Vlog And A Blog
May 12, 2025
-
Sum Of Angles In A Hexagon
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 4 6 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.