What Is The Lcm Of 3 And 5
Juapaving
Apr 01, 2025 · 4 min read
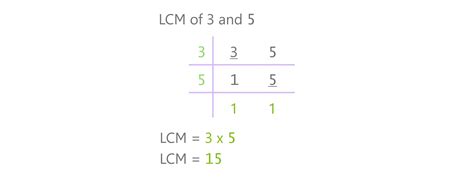
Table of Contents
What is the LCM of 3 and 5? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly in arithmetic and number theory. It has practical applications in various fields, from scheduling to simplifying fractions. This article delves deep into the concept of LCM, focusing specifically on the LCM of 3 and 5, while providing broader context and exploring different methods for calculating LCMs. We'll explore the definition, multiple methods of calculation, practical applications, and even touch upon the LCM's role in more advanced mathematical concepts.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3. Understanding LCMs is crucial for solving problems involving fractions, ratios, and cyclic events.
Key Differences Between LCM and GCF (Greatest Common Factor)
It's important to distinguish the LCM from the greatest common factor (GCF), also known as the greatest common divisor (GCD). While the LCM finds the smallest common multiple, the GCF finds the largest common factor. For instance, the GCF of 12 and 18 is 6, as 6 is the largest number that divides both 12 and 18. The LCM and GCF are related; for any two positive integers a and b, the product of their LCM and GCF is equal to the product of the two numbers (LCM(a,b) * GCF(a,b) = a * b).
Calculating the LCM of 3 and 5
Now, let's address the specific question: What is the LCM of 3 and 5? We can employ several methods to determine this.
Method 1: Listing Multiples
The simplest method, especially for smaller numbers like 3 and 5, is to list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
By comparing the lists, we see that the smallest number appearing in both lists is 15. Therefore, the LCM of 3 and 5 is 15.
Method 2: Prime Factorization
This method is more efficient for larger numbers. We first find the prime factorization of each number.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 5: 5 (5 is a prime number)
Since 3 and 5 are both prime numbers and have no common factors, their LCM is simply their product.
LCM(3, 5) = 3 x 5 = 15
Method 3: Formula Using GCF
As mentioned earlier, the LCM and GCF are related. We can use the formula:
LCM(a, b) = (a * b) / GCF(a, b)
Since 3 and 5 are both prime numbers, their GCF is 1. Therefore:
LCM(3, 5) = (3 * 5) / 1 = 15
Practical Applications of LCM
The concept of LCM finds applications in various real-world scenarios. Here are a few examples:
Scheduling and Timing
Imagine you have two machines that operate on different cycles. One machine completes a cycle every 3 minutes, and the other every 5 minutes. To find out when both machines will complete a cycle simultaneously, you need to find the LCM of 3 and 5. The LCM is 15, meaning both machines will complete a cycle at the same time after 15 minutes.
Fraction Addition and Subtraction
To add or subtract fractions with different denominators, we need to find a common denominator, which is typically the LCM of the denominators. For instance, adding 1/3 and 1/5 requires finding the LCM of 3 and 5, which is 15. The fractions then become 5/15 and 3/15, allowing for easy addition (5/15 + 3/15 = 8/15).
Pattern Recognition and Cyclic Events
LCM is useful in identifying repeating patterns or cyclic events. For example, if two events occur periodically (say, every 3 days and every 5 days), finding the LCM determines when both events coincide.
LCM in Advanced Mathematics
The concept of LCM extends beyond basic arithmetic. It plays a significant role in:
Abstract Algebra
In abstract algebra, the LCM finds applications in the study of rings and ideals. The concept generalizes to more complex algebraic structures.
Number Theory
The LCM is a fundamental tool in number theory, used in various proofs and theorems related to divisibility and prime factorization.
Modular Arithmetic
LCMs are crucial in modular arithmetic, used to solve congruences and related problems.
Conclusion: The Importance of Understanding LCM
The LCM, a seemingly simple concept, is a powerful tool with broad applications across various mathematical fields and practical scenarios. Understanding how to calculate the LCM, particularly for simpler cases like the LCM of 3 and 5, lays the foundation for tackling more complex mathematical problems and real-world challenges involving cyclical events, fraction manipulation, and scheduling. Mastering the different methods for calculating the LCM, from listing multiples to prime factorization and utilizing the GCF relationship, provides a versatile toolkit for approaching diverse mathematical problems effectively. The LCM of 3 and 5, being 15, is just a stepping stone to understanding this fundamental concept and its wide-reaching implications.
Latest Posts
Latest Posts
-
How Many Miles Are In 10 Kilometers
Apr 02, 2025
-
Where In A Plant Cell Does Photosynthesis Occur
Apr 02, 2025
-
A Motor And A Generator Are
Apr 02, 2025
-
Allows Materials In And Out Of The Cell
Apr 02, 2025
-
Which Of The Following Is Matched Correctly
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 3 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
