What Is The Lcm Of 3 And 15
Juapaving
May 12, 2025 · 5 min read
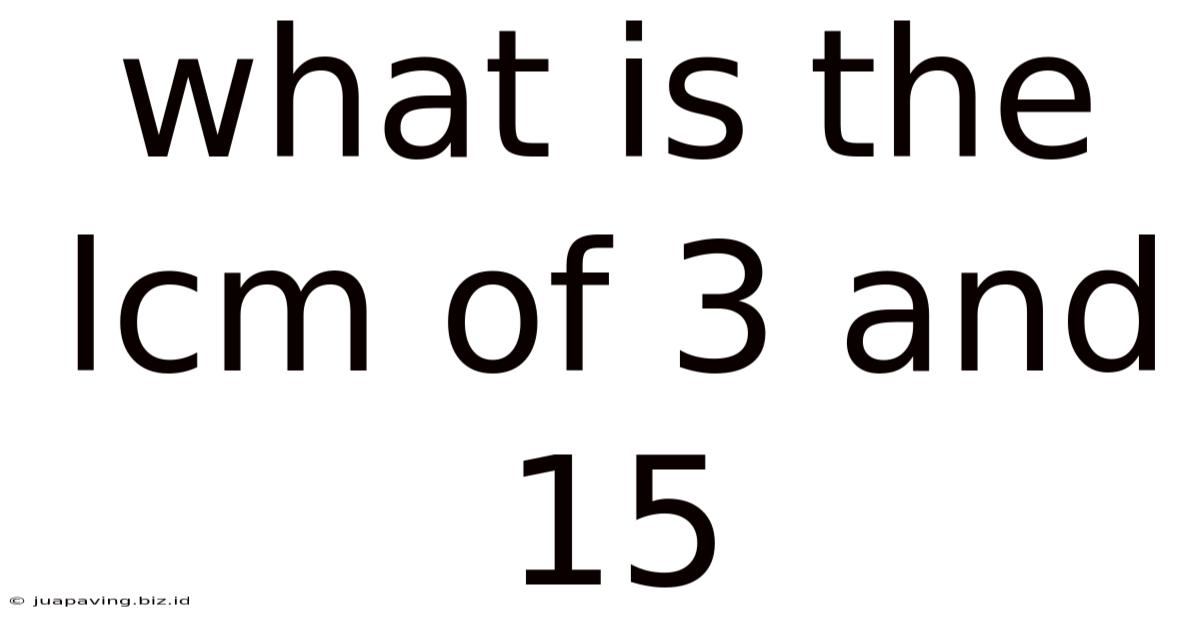
Table of Contents
What is the LCM of 3 and 15? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it lays a strong foundation for more advanced mathematical concepts. This article will explore the LCM of 3 and 15 in detail, covering multiple approaches and illustrating their applications in various scenarios. We'll also delve into the broader significance of LCMs in mathematics and beyond.
Understanding Least Common Multiples (LCM)
Before we tackle the specific LCM of 3 and 15, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. This means that the LCM is a common multiple, meaning it's a multiple of each of the numbers, and it's the least of these common multiples.
Consider the multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30... Now consider the multiples of 15: 15, 30, 45, 60, 75...
Notice that 15 appears in both lists. It's a common multiple. Furthermore, it's the smallest common multiple. Therefore, the LCM of 3 and 15 is 15.
Method 1: Listing Multiples
The method we just used is the simplest approach, especially for smaller numbers. It involves listing the multiples of each number until you find the smallest common multiple. This method is intuitive and easy to visualize, making it ideal for beginners or when working with small numbers. However, it becomes less efficient as the numbers get larger.
Steps:
- List the multiples of the first number (3): 3, 6, 9, 12, 15, 18, 21...
- List the multiples of the second number (15): 15, 30, 45...
- Identify the smallest number that appears in both lists (15).
Therefore, the LCM(3, 15) = 15.
Method 2: Prime Factorization
A more efficient method, particularly for larger numbers, is using prime factorization. This involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Steps:
-
Find the prime factorization of each number:
- 3 = 3¹ (3 is already a prime number)
- 15 = 3¹ × 5¹
-
Identify the highest power of each prime factor:
- The prime factors are 3 and 5.
- The highest power of 3 is 3¹
- The highest power of 5 is 5¹
-
Multiply the highest powers together:
- LCM(3, 15) = 3¹ × 5¹ = 15
This method is more systematic and works well for larger numbers where listing multiples would become cumbersome. It provides a clear and structured approach to finding the LCM.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. There's a formula that connects the LCM and GCD:
LCM(a, b) × GCD(a, b) = a × b
Let's use this formula for our example:
-
Find the GCD of 3 and 15: The greatest common divisor of 3 and 15 is 3.
-
Apply the formula:
- LCM(3, 15) × GCD(3, 15) = 3 × 15
- LCM(3, 15) × 3 = 45
- LCM(3, 15) = 45 / 3 = 15
This method highlights the interconnectedness between LCM and GCD, offering another powerful approach to solving the problem. Finding the GCD can sometimes be easier than directly finding the LCM, especially when dealing with larger numbers. Algorithms like the Euclidean algorithm provide efficient ways to calculate the GCD.
Real-World Applications of LCM
Understanding LCMs isn't just about abstract mathematical concepts; it has practical applications in various fields:
-
Scheduling: Imagine you have two machines that operate on different cycles. One machine runs every 3 hours, and the other runs every 15 hours. The LCM (15 hours) tells you when both machines will run simultaneously again. This is crucial in scheduling tasks and optimizing processes.
-
Fraction Arithmetic: When adding or subtracting fractions with different denominators, finding the LCM of the denominators helps determine the least common denominator (LCD), simplifying the calculation process.
-
Music Theory: In music, rhythms and patterns often repeat. The LCM helps determine when rhythms will coincide, important in understanding musical harmony and composition.
-
Construction and Engineering: In projects involving repetitive patterns or cycles, LCM is crucial for efficient planning and resource allocation.
-
Computer Science: In algorithms and data structures, the concept of LCM appears in problems related to cycle detection and synchronization.
Expanding the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly effective. For example, to find the LCM of 3, 15, and 5:
-
Prime Factorization:
- 3 = 3¹
- 15 = 3¹ × 5¹
- 5 = 5¹
-
Highest Powers:
- 3¹
- 5¹
-
Multiplication:
- LCM(3, 15, 5) = 3¹ × 5¹ = 15
Conclusion: Mastering the LCM
Finding the least common multiple is a fundamental skill with wide-ranging applications. While the simple method of listing multiples works well for small numbers, the prime factorization method offers a more efficient and systematic approach for larger numbers. Understanding the relationship between LCM and GCD provides another valuable tool. By mastering these techniques, you'll not only improve your arithmetic skills but also gain a deeper understanding of mathematical principles with real-world relevance. The seemingly simple question of "What is the LCM of 3 and 15?" opens a door to a wealth of mathematical concepts and applications. Remember, consistent practice and exploration of different methods are key to solidifying your understanding and becoming proficient in finding LCMs.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 3 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.