What Is The Lcm Of 28 And 42
Juapaving
May 14, 2025 · 4 min read
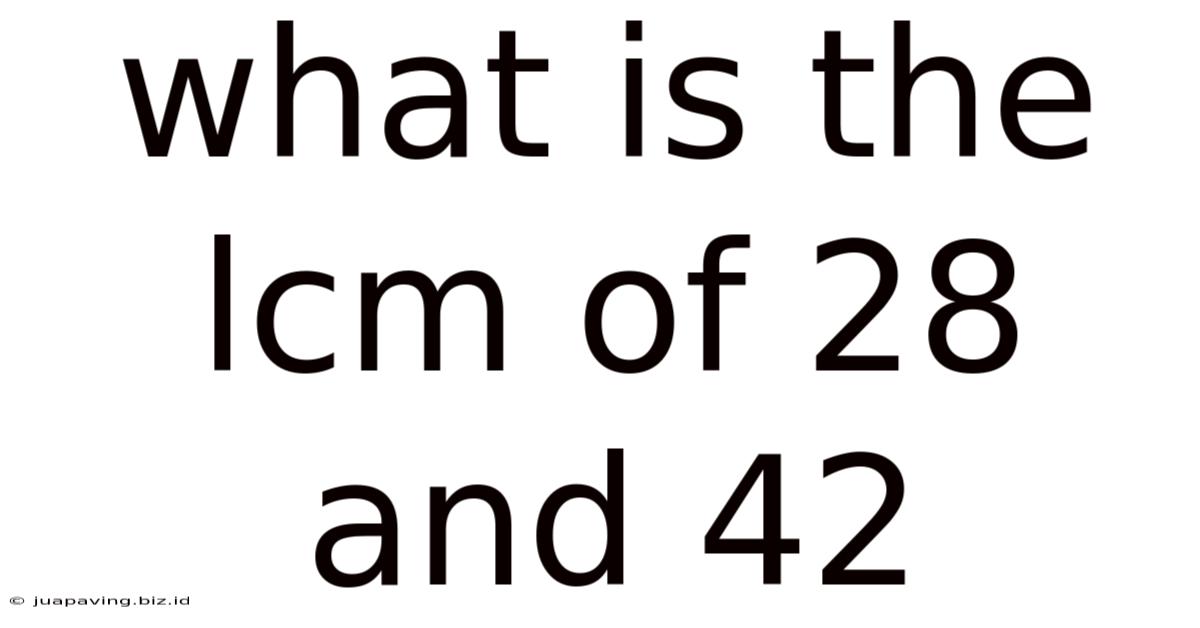
Table of Contents
What is the LCM of 28 and 42? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it is crucial for a strong foundation in mathematics. This comprehensive guide explores the LCM of 28 and 42, delving into different approaches, their applications, and related mathematical concepts. We'll go beyond just finding the answer and delve into the why behind the methods.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 28 and 42, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers as factors.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10... and multiples of 3 are 3, 6, 9, 12... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Methods for Finding the LCM
Several methods exist for calculating the LCM of two or more numbers. We'll explore the most common ones, applying them to find the LCM of 28 and 42.
1. Listing Multiples Method
This is a straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both lists.
- Multiples of 28: 28, 56, 84, 112, 140, 168, ...
- Multiples of 42: 42, 84, 126, 168, 210, ...
Notice that 84 appears in both lists. However, a smaller common multiple, 84, appears first. Therefore, the LCM(28, 42) = 84. This method works well for smaller numbers but becomes inefficient for larger numbers.
2. Prime Factorization Method
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
Let's find the prime factorization of 28 and 42:
- 28 = 2² x 7¹
- 42 = 2¹ x 3¹ x 7¹
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2² = 4
- Highest power of 3: 3¹ = 3
- Highest power of 7: 7¹ = 7
Now, multiply these highest powers together: 4 x 3 x 7 = 84.
Therefore, the LCM(28, 42) = 84 using the prime factorization method. This method is generally preferred for its efficiency and applicability to larger numbers.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The relationship is given by the formula:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 28 and 42. We can use the Euclidean algorithm for this:
- Divide 42 by 28: 42 = 28 x 1 + 14
- Divide 28 by 14: 28 = 14 x 2 + 0
The last non-zero remainder is the GCD, which is 14.
Now, we can use the formula:
LCM(28, 42) = (28 x 42) / GCD(28, 42) = (28 x 42) / 14 = 84
Therefore, the LCM(28, 42) = 84 using the GCD method. This method is efficient and relies on a well-established algorithm for finding the GCD.
Applications of LCM
Understanding and calculating LCMs has numerous applications across various fields:
- Scheduling: Determining when events will occur simultaneously. For example, if two buses arrive at a stop every 28 and 42 minutes respectively, they will arrive together every 84 minutes (the LCM).
- Fraction Operations: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is essentially the LCM of the denominators.
- Modular Arithmetic: LCM plays a vital role in solving problems related to congruences and remainders.
- Music Theory: Determining the least common multiple of note durations is crucial in music composition and analysis.
- Engineering and Construction: Calculating optimal timings and cycles in various engineering applications.
Beyond the Basics: Exploring Further
The calculation of the LCM extends beyond just two numbers. You can find the LCM of multiple numbers by extending the prime factorization method or using iterative GCD calculations. For instance, to find the LCM of 28, 42, and say, 21:
-
Prime Factorization:
- 28 = 2² x 7
- 42 = 2 x 3 x 7
- 21 = 3 x 7
-
Identify Highest Powers:
- 2²
- 3¹
- 7¹
-
Calculate LCM: 2² x 3 x 7 = 84
Therefore, the LCM(28, 42, 21) = 84.
Conclusion: Mastering LCM Calculations
Finding the LCM of 28 and 42, as we've demonstrated, can be approached using multiple methods. The choice of method often depends on the size of the numbers involved and personal preference. The prime factorization method generally provides efficiency and clarity, especially when dealing with larger numbers or multiple numbers simultaneously. Understanding the underlying concepts and various methods not only helps in solving specific problems but also builds a strong mathematical foundation applicable across diverse fields. Remember, the key is to grasp the fundamental meaning of LCM and to choose the most appropriate and efficient method for the task at hand. This deep dive has equipped you with the knowledge to confidently tackle LCM calculations in any context.
Latest Posts
Latest Posts
-
5 Letter Word With I E
May 14, 2025
-
Five Letter Words Starting With Ad
May 14, 2025
-
How Many Valence Electrons Does Sodium Have
May 14, 2025
-
Balanced Equation Of Sodium Hydroxide And Sulfuric Acid
May 14, 2025
-
Describing Words That Begin With E
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 28 And 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.