What Is The Lcm Of 25 And 30
Juapaving
May 11, 2025 · 5 min read
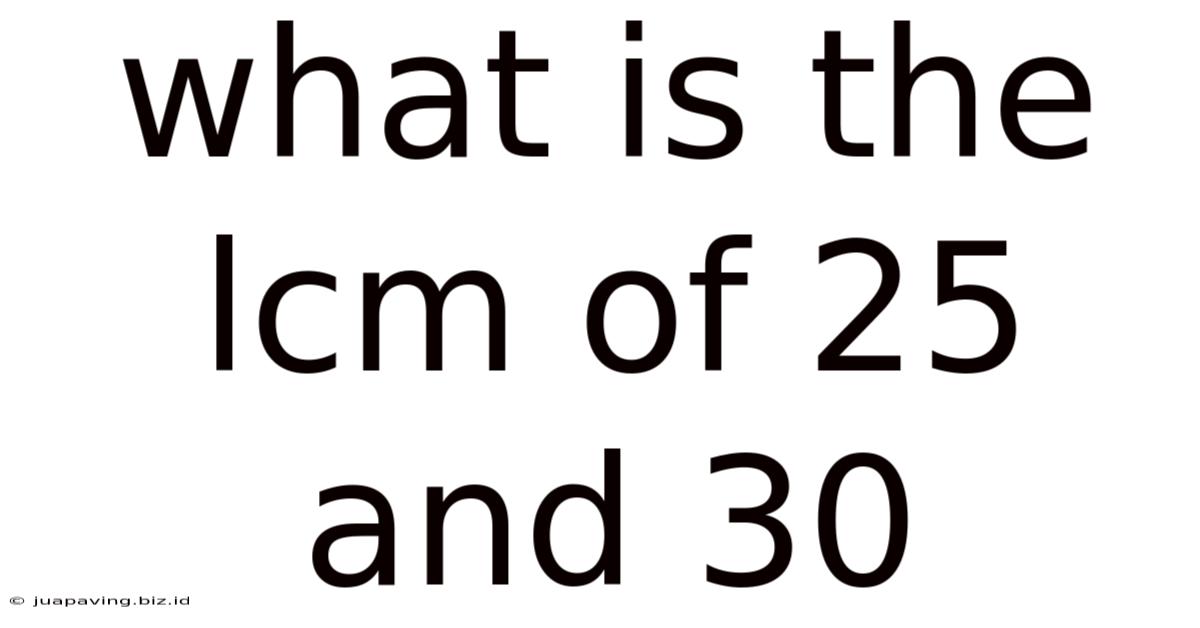
Table of Contents
What is the LCM of 25 and 30? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics with applications ranging from simple fraction arithmetic to complex scheduling problems. This article will not only answer the question "What is the LCM of 25 and 30?" but also provide a comprehensive understanding of LCMs, exploring different methods for calculating them and illustrating their practical significance.
Understanding Least Common Multiples (LCMs)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
Understanding LCMs is crucial for various mathematical operations, including:
- Adding and subtracting fractions: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators.
- Solving problems involving cycles or periodic events: LCMs are essential for determining when events with different cycles will occur simultaneously. For instance, determining when two machines operating at different speeds will complete their cycles at the same time.
- Simplifying algebraic expressions: LCMs can simplify algebraic expressions involving fractions.
Methods for Calculating the LCM
Several methods can be used to calculate the LCM of two or more numbers. We'll explore the most common ones:
1. Listing Multiples Method
This method involves listing the multiples of each number until you find the smallest multiple common to both. Let's illustrate this with the numbers 25 and 30:
Multiples of 25: 25, 50, 75, 100, 125, 150, 175, 200... Multiples of 30: 30, 60, 90, 120, 150, 180, 210...
The smallest multiple common to both lists is 150. Therefore, the LCM of 25 and 30 is 150.
This method is simple for smaller numbers but can become cumbersome for larger numbers with many multiples.
2. Prime Factorization Method
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
Let's apply this method to find the LCM of 25 and 30:
- Prime factorization of 25: 5²
- Prime factorization of 30: 2 × 3 × 5
To find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2¹ (from 30).
- The highest power of 3 is 3¹ (from 30).
- The highest power of 5 is 5² (from 25).
Therefore, the LCM of 25 and 30 is 2¹ × 3¹ × 5² = 2 × 3 × 25 = 150.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are related by the formula:
LCM(a, b) × GCD(a, b) = a × b
We can use this relationship to find the LCM if we know the GCD. Let's find the GCD of 25 and 30 using the Euclidean algorithm:
- Divide 30 by 25: 30 = 25 × 1 + 5
- Divide 25 by the remainder 5: 25 = 5 × 5 + 0
The GCD is the last non-zero remainder, which is 5.
Now, using the formula:
LCM(25, 30) × GCD(25, 30) = 25 × 30 LCM(25, 30) × 5 = 750 LCM(25, 30) = 750 / 5 = 150
Practical Applications of LCM
The concept of LCM has numerous practical applications across various fields:
1. Scheduling and Synchronization
Imagine two machines in a factory. One completes a cycle every 25 minutes, and the other every 30 minutes. To determine when both machines will complete a cycle simultaneously, we need to find the LCM of 25 and 30. The LCM is 150, meaning both machines will complete a cycle at the same time after 150 minutes.
2. Fraction Arithmetic
When adding or subtracting fractions with different denominators, we need to find a common denominator. This common denominator is the LCM of the original denominators. For example, to add 1/25 and 1/30, we find the LCM of 25 and 30 (which is 150). We then rewrite the fractions with 150 as the denominator:
1/25 = 6/150 1/30 = 5/150
Now we can add them easily: 6/150 + 5/150 = 11/150
3. Music Theory
LCMs are used in music theory to determine the least common multiple of the periods of different musical rhythms or patterns. This helps in coordinating the rhythmic structure of musical compositions.
4. Gear Ratios
In mechanical engineering, LCM is used to calculate gear ratios to achieve specific speed or torque requirements.
Beyond Two Numbers: LCM of Multiple Integers
The methods discussed above can be extended to find the LCM of more than two numbers. The prime factorization method is generally the most efficient approach for multiple numbers. For example, to find the LCM of 12, 18, and 30:
- Prime factorization of 12: 2² × 3
- Prime factorization of 18: 2 × 3²
- Prime factorization of 30: 2 × 3 × 5
The LCM is 2² × 3² × 5 = 4 × 9 × 5 = 180
Conclusion: Mastering LCM Calculations
Calculating the least common multiple is a fundamental skill with broad applications. While the listing multiples method works for smaller numbers, the prime factorization method offers a more efficient and scalable approach, particularly for larger numbers and multiple integers. Understanding LCM is crucial not only for solving mathematical problems but also for tackling real-world scenarios involving scheduling, synchronization, and various other applications across different fields. By mastering these methods, you equip yourself with a powerful tool for problem-solving in diverse contexts. Remember, the LCM of 25 and 30, as we've demonstrated through multiple methods, is definitively 150.
Latest Posts
Latest Posts
-
Which Element Is The Most Reactive Nonmetal
May 11, 2025
-
Has Properties Of Both Metals And Nonmetals
May 11, 2025
-
Difference Between Sodium Bicarbonate And Sodium Carbonate
May 11, 2025
-
Translate The Triangle Then Enter The New Coordinates
May 11, 2025
-
Which Form Of Matter Is Usually The Densest
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 25 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.